Теория кабеля

Рисунок. 1: Упрощенный вид нейронного волокна в теории кабеля

Классическая теория кабеля использует математические модели для вычисления электрического тока (и сопутствующего напряжения ) вдоль пассивных нейритов, особенно дендритов, которые получают синаптические входные данные в разных местах и ​​в разное время. Оценки сделаны путем моделирования дендритов и аксонов в виде цилиндров, состоящих из сегментов с емкостями $см\; \{\backslash \; displaystyle\; c\_\; \{m\}\}$и сопротивлениями. $rm\; \{\backslash \; displaystyle\; r\_\; \{m\}\}$, объединенные параллельно (см. Рис. 1). Емкость нейронного волокна возникает из-за того, что электростатические силы действуют через очень тонкий липидный бислой (см. Рисунок 2). Сопротивление последовательно вдоль волокна $rl\; \{\backslash \; displaystyle\; r\_\; \{l\}\}$происходит из-за значительного сопротивления аксоплазмы движению электрического заряда.

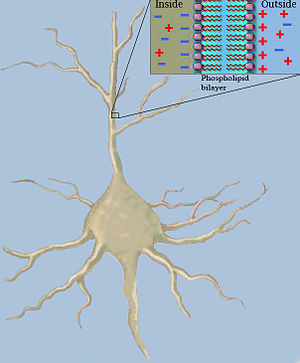
Рисунок. 2: Емкость волокна

• 1 История
• 2 Получение уравнения кабеля
• 3 Константа длины
• 4 Постоянная времени
• 5 Общая форма и математическая структура
• 6 См. Также
• 7 источников
• 8 заметок

Теория кабеля в вычислительной нейробиологии уходит корнями в 1850-е годы, когда профессор Уильям Томсон (позже известный как лорд Кельвин) начал разработку математических моделей затухания сигнала в подводных (подводных) телеграфных кабелях. Эти модели напоминали уравнения в частных производных, используемые Фурье для описания теплопроводности в проводе.

1870-е годы были отмечены первыми попытками Германа смоделировать нейрональные электротонические потенциалы, также сосредоточившись на аналогиях с теплопроводностью. Однако именно Хорвег первым открыл аналогии с подводными кабелями Кельвина в 1898 году, а затем Герман и Кремер независимо разработали теорию кабеля для нейронных волокон в начале 20 века. Дальнейшие математические теории проводимости нервных волокон, основанные на теории кабеля, были разработаны Коул и Ходжкин (1920–1930-е годы), Offner et al. (1940) и Раштон (1951).

Экспериментальные доказательства важности кабельной теории в моделировании поведения аксонов начали появляться в 1930-х годах благодаря работе Коула, Кертиса, Ходжкина, сэра Бернарда Каца, Раштон, Тасаки и другие. Две ключевые работы этой эпохи - это работы Дэвиса и Лоренте де Но (1947) и Ходжкина и Раштона (1946).

В 1950-х годах были усовершенствованы методы измерения электрической активности отдельных нейронов. Таким образом, кабельная теория стала важной для анализа данных, собранных из записей внутриклеточных микроэлектродов, и для анализа электрических свойств нейрональных дендритов. Такие ученые, как Кумбс, Экклс, Фатт, Фрэнк, Фуортес и другие, теперь в значительной степени полагались на теорию кабеля, чтобы получить функциональную информацию о нейронах и направить их при разработке новых экспериментов.

Позже теория кабеля с ее математическими производными позволила исследовать все более сложные модели нейронов, такие как Джек, Ралл, Редман, Ринзель, Идан Сегев, Таквелл, Белл и Ианнелла.

Обратите внимание, что существуют различные соглашения для r m. Здесь r m и c m, как введено выше, измеряются на единицу длины мембраны (на метр (м)). Таким образом, r м измеряется в Ом · метрах (Ом · м), а c м в фарадах на метр (Ф / м).. Это контрастирует с R м (в Ом · м²) и C м (в Ф / м²), которые представляют собой удельное сопротивление и емкость соответственно одной единицы площади мембраны ( в м). Таким образом, если известен радиус аксона a, то его окружность равна 2πa, а его значения r m и его значения c m могут быть вычислены как:

$rm\; =\; р\; м\; 2\; \pi \; a\; \{\backslash \; displaystyle\; r\_\; \{m\}\; =\; \{\backslash \; frac\; \{R\_\; \{m\}\}\; \{2\; \backslash \; pi\; a\; \backslash \}\}\}$

(1)

$cm\; =\; C\; m\; 2\; \pi \; a\; \{\; \backslash \; displaystyle\; c\_\; \{m\}\; =\; C\_\; \{m\}\; 2\; \backslash \; pi\; a\; \backslash \}$

(2)

Эти отношения интуитивно понятны, потому что чем больше окружность аксона, тем больше площадь, через которую проходит заряд. его мембрана, и, следовательно, более низкое сопротивление мембраны (деление R m на 2πa); и больше мембраны, доступной для хранения заряда (умножение C m на 2πa). удельное электрическое сопротивление, ρ l, аксоплазмы позволяет рассчитать продольное внутриклеточное сопротивление на единицу длины, r l, (в Ом · м) по уравнению:

$rl\; =\; \rho \; l\; \pi \; a\; 2\; \{\backslash \; displaystyle\; r\_\; \{l\}\; =\; \{\backslash \; frac\; \{\backslash \; rho\; \_\; \{l\}\}\; \{\backslash \; pi\; a\; ^\; \{2\}\; \backslash \}\}\}$

(3)

Чем больше площадь поперечного сечения аксона, πa², тем больше путей для прохождения заряда через его аксоплазму и тем ниже аксоплазматическое сопротивление.

В нескольких важных направлениях развития классической кабельной теории недавно были введены эндогенные структуры для анализа эффектов поляризации белков внутри дендритов и различных распределений синаптических входных сигналов по дендритной поверхности нейрона.

Чтобы лучше понять, как выводится уравнение кабеля, сначала еще больше упростите теоретический нейрон и представьте, что он имеет идеально герметичную мембрану (r m = ∞) без потери тока на снаружи и без емкости (c м = 0). Ток, вводимый в волокно в позиции x = 0, будет двигаться по внутренней части волокна без изменений. Двигаясь от точки впрыска и используя закон Ома (V = IR), мы можем рассчитать изменение напряжения как:

$\Delta \; V\; =\; -\; ilrl\; \Delta \; x\; \{\backslash \; displaystyle\; \backslash \; Delta\; V\; =\; -i\_\; \{l\}\; r\_\; \{l\}\; \backslash \; Delta\; x\; \backslash \}$

(4)

где отрицательное значение означает, что ток течет вниз по градиенту потенциала.

Если Δx стремится к нулю и имеет бесконечно малые приращения x, можно записать (4) как:

$\partial \; V\; \partial \; x\; =\; -\; ilrl\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; V\}\; \{\backslash \; partial\; x\}\}\; =\; -\; i\_\; \{l\}\; r\_\; \{l\}\; \backslash \}$

(5)

или

$1\; rl\; \partial \; V\; \partial \; x\; =\; -\; il\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{\; r\_\; \{l\}\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; V\}\; \{\backslash \; partial\; x\}\}\; =\; -\; i\_\; \{l\}\; \backslash \}$

(6)

Возвращение r m обратно в картинку это все равно что проделывать дыры в садовом шланге. Чем больше отверстий, тем быстрее вода вытечет из шланга и тем меньше воды пройдет от начала шланга до конца. Точно так же в аксоне часть тока, проходящего в продольном направлении через аксоплазму, будет уходить через мембрану.

Если i m - ток, уходящий через мембрану на единицу длины, м, то общий ток, уходящий вдоль y единиц, должен быть y · i m. Таким образом, изменение тока в аксоплазме Δi l на расстоянии Δx от положения x = 0 можно записать как:

$\Delta \; il\; =\; -\; im\; \Delta \; x\; \{\backslash \; displaystyle\; \backslash \; Delta\; i\_\; \{l\}\; =\; -\; i\_\; \{m\}\; \backslash \; Delta\; x\; \backslash \}$

(7)

или, используя непрерывные, бесконечно малые приращения:

$\partial \; il\; \partial \; x\; =\; -\; im\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; частичное\; i\_\; \{l\}\}\; \{\backslash \; partial\; x\}\}\; =\; -\; i\_\; \{m\}\; \backslash \}$

(8)

$im\; \{\backslash \; displaystyle\; i\_\; \{m\}\}$может быть выражено еще одним формула, включая емкость. Емкость вызовет поток заряда (тока) к мембране на стороне цитоплазмы. Этот ток обычно называют током смещения (здесь обозначается $i\; c\; \{\backslash \; displaystyle\; i\_\; \{c\}\}$.) Поток будет иметь место только до тех пор, пока не будет достигнута емкость мембраны. $ic\; \{\backslash \; displaystyle\; i\_\; \{c\}\}$тогда можно выразить как:

$ic\; =\; cm\; \partial \; V\; \partial \; t\; \{\backslash \; displaystyle\; i\_\; \{c\}\; =\; c\_\; \{m\}\; \{\backslash \; frac\; \{\; \backslash \; partial\; V\}\; \{\backslash \; partial\; t\}\}\; \backslash \}$

(9)

где $cm\; \{\backslash \; displaystyle\; c\_\; \{m\}\}$- емкость мембраны, а $\partial \; V\; /\; \partial \; t\; \{\backslash \; displaystyle\; \{\backslash \; partial\; V\}\; /\; \{\backslash \; partial\; t\}\}$- изменение напряжения во времени. Ток, который проходит через мембрану ($ir\; \{\backslash \; displaystyle\; i\_\; \{r\}\}$), можно выразить как:

$ir\; =\; V\; rm\; \{\backslash \; displaystyle\; i\_\; \{r\}\; =\; \{\backslash \; frac\; \{\; V\}\; \{r\_\; \{m\}\}\}\}$

(10)

и поскольку $im\; =\; ir\; +\; ic\; \{\backslash \; displaystyle\; i\_\; \{m\}\; =\; i\_\; \{r\}\; +\; i\_\; \{c\}\}$следующее уравнение для $im\; \{\backslash \; displaystyle\; i\_\; \{m\}\}$может быть получено, если от электрода не добавляется дополнительный ток:

$\partial \; il\; \partial \; x\; =\; -\; im\; =\; -\; (V\; rm\; +\; см\; \partial \; V\; \partial \; T)\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; i\_\; \{l\}\}\; \{\backslash \; partial\; x\}\}\; =\; -\; i\_\; \{m\}\; =\; -\; \backslash \; left\; (\{\backslash \; frac\; \{V\}\; \{r\_\; \{\; m\}\}\}\; +\; c\_\; \{m\}\; \{\backslash \; frac\; \{\backslash \; partial\; V\}\; \{\backslash \; partial\; t\}\}\; \backslash \; right)\}$

(11)

где $\partial \; il\; /\; \partial \; x\; \{\backslash \; displaystyle\; \{\backslash \; partial\; i\_\; \{l\}\}\; /\; \{\backslash \; partial\; x\}\}$представляет изменение продольного тока на единицу длины.

Объединение уравнений (6) и (11) дает первую версию уравнения кабеля:

$1\; rl\; \partial \; 2\; V\; \partial \; x\; 2\; =\; cm\; \partial \; V\; \partial \; t\; +\; V\; rm\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{r\_\; \{l\}\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; V\}\; \{\backslash \; partial\; x\; ^\; \{2\}\}\}\; =\; c\_\; \{m\}\; \{\backslash \; frac\; \{\backslash \; partial\; V\}\; \{\; \backslash \; partial\; t\}\}\; +\; \{\backslash \; frac\; \{V\}\; \{r\_\; \{m\}\}\}\}$

(12)

, которое является уравнением в частных производных (PDE) второго порядка.

Путем простой перестановки уравнения (12) (см. Ниже) можно получить два важных члена, а именно постоянную длины (иногда называемую пространственной постоянной), обозначенную $\lambda \; \{\; \backslash \; displaystyle\; \backslash \; lambda\}$и постоянная времени, обозначенная $\tau \; \{\backslash \; displaystyle\; \backslash \; tau\}$. Следующие разделы посвящены этим условиям.

Константа длины, $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$(лямбда), является параметром, который указывает, насколько сильно будет влиять стационарный ток напряжение по кабелю. Чем больше значение $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$, тем дальше будет течь заряд. Константа длины может быть выражена как:

$\lambda \; =\; rmrl\; \{\backslash \; displaystyle\; \backslash \; lambda\; =\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{r\_\; \{m\}\}\; \{r\_\; \{l\}\}\}\}\}$

(13)

Чем больше сопротивление мембраны, r m, тем больше значение $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$, и тем больше ток останется внутри аксоплазмы, чтобы пройти через нее в продольном направлении. аксон. Чем выше аксоплазматическое сопротивление, $rl\; \{\backslash \; displaystyle\; r\_\; \{l\}\}$, чем меньше значение $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$, тем сложнее будет для тока проходить через аксоплазму, и тем короче ток сможет пройти. Можно решить уравнение (12) и прийти к следующему уравнению (которое действительно в стационарных условиях, т. Е. Когда время приближается к бесконечности):

$V\; x\; =\; V\; 0\; e\; -\; x\; \lambda \; \{\backslash \; displaystyle\; V\_\; \{x\}\; =\; V\_\; \{0\}\; e\; ^\; \{-\; \{\backslash \; frac\; \{x\}\; \{\backslash \; lambda\}\}\}\}$

(14)

где $V\; 0\; \{\backslash \; displaystyle\; V\_\; \{0\}\}$- деполяризация в $x\; =\; 0\; \{\backslash \; displaystyle\; x\; =\; 0\}$(точка подачи тока), e - экспоненциальная константа (приблизительное значение 2,71828) и $V\; x\; \{\backslash \; displaystyle\; V\_\; \{x\}\}$- напряжение на заданном расстоянии x от x = 0. Когда $x\; =\; \lambda \; \{\backslash \; displaystyle\; x\; =\; \backslash \; lambda\}$, тогда

$x\; \lambda \; =\; 1\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{x\}\; \{\backslash \; lambda\}\}\; =\; 1\}$

( 15)

и

$V\; x\; =\; V\; 0\; e\; -\; 1\; \{\backslash \; displaystyle\; V\_\; \{x\}\; =\; V\_\; \{0\}\; e\; ^\; \{-\; 1\}\}$

(16)

, что означает, что когда мы мера $V\; \{\backslash \; displaystyle\; V\}$на расстоянии $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$от $x\; =\; 0\; \{\backslash \; displaystyle\; x\; =\; 0\}$получаем

$V\; \lambda \; =\; V\; 0\; e\; =\; 0,368\; V\; 0\; \{\backslash \; displaystyle\; V\; \_\; \{\backslash \; lambda\}\; =\; \{\backslash \; frac\; \{V\_\; \{0\}\}\; \{e\}\}\; =\; 0,368V\_\; \{0\}\}$

(17)

Таким образом, $V\; \lambda \; \{\backslash \; displaystyle\; V\; \_\; \{\backslash \; lambda\}\}$всегда составляет 36,8% от $V\; 0\; \{\backslash \; displaystyle\; V\_\; \{0\}\}$.

Нейробиологов часто интересует, насколько быстро мембранный потенциал, $V\; m\; \{\backslash \; displaystyle\; V\_\; \{m\}\}$, аксона изменяется в ответ на изменения тока вводится в аксоплазму. Постоянная времени $\tau \; \{\backslash \; displaystyle\; \backslash \; tau\}$- это индекс, который предоставляет информацию об этом значении. $\tau \; \{\backslash \; displaystyle\; \backslash \; tau\}$можно рассчитать как:

$\tau \; =\; r\; m\; c\; m.\; \{\backslash \; displaystyle\; \backslash \; tau\; =\; r\_\; \{m\}\; c\_\; \{m\}.\; \backslash \}$

(18)

Чем больше емкость мембраны, $см\; \{\backslash \; displaystyle\; c\_\; \{m\}\}$, чем больше тока требуется для зарядки и разрядки участка мембраны, и тем дольше будет этот процесс. Чем больше сопротивление мембраны $r\; m\; \{\backslash \; displaystyle\; r\_\; \{m\}\}$, тем труднее току вызвать изменение мембранного потенциала. Таким образом, чем выше $\tau \; \{\backslash \; displaystyle\; \backslash \; tau\}$, тем медленнее может двигаться нервный импульс. Это означает, что мембранный потенциал (напряжение на мембране) больше отстает от инжектируемого тока. Время отклика варьируется от 1–2 миллисекунд в нейронах, обрабатывающих информацию, требующую высокой временной точности, до 100 миллисекунд и более. Типичное время отклика составляет около 20 миллисекунд.

Если умножить уравнение (12) на $rm\; \{\backslash \; displaystyle\; r\_\; \{m\}\}$с обеих сторон знак равенства получаем:

$rmrl\; \partial \; 2\; V\; \partial \; x\; 2\; =\; cmrm\; \partial \; V\; \partial \; t\; +\; V\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{r\_\; \{m\}\}\; \{r\_\; \{l\}\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{\; 2\}\; V\}\; \{\backslash \; partial\; x\; ^\; \{2\}\}\}\; =\; c\_\; \{m\}\; r\_\; \{m\}\; \{\backslash \; frac\; \{\backslash \; partial\; V\}\; \{\backslash \; partial\; t\}\}\; +\; V\}$

(19)

и распознать $\lambda \; 2\; =\; rm\; /\; rl\; \{\backslash \; displaystyle\; \backslash \; lambda\; ^\; \{2\}\; =\; \{r\_\; \{m\}\}\; /\; \{r\_\; \{l\}\}\}$слева и $\tau \; =\; cmrm\; \{\backslash \; displaystyle\; \backslash \; tau\; =\; c\_\; \{m\}\; r\_\; \{m\}\}$с правой стороны. Уравнение кабеля теперь может быть записано в его, пожалуй, наиболее известной форме:

$\lambda \; 2\; \partial \; 2\; V\; \partial \; x\; 2\; =\; \tau \; \partial \; V\; \partial \; t\; +\; V\; \{\backslash \; displaystyle\; \backslash \; lambda\; ^\; \{2\}\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{\; 2\}\; V\}\; \{\backslash \; partial\; x\; ^\; \{2\}\}\}\; =\; \backslash \; tau\; \{\backslash \; frac\; \{\backslash \; partial\; V\}\; \{\backslash \; partial\; t\}\}\; +\; V\}$

(20)

Это 1D Уравнение теплопроводности или Уравнение диффузии, для которого были разработаны многие методы решения, такие как функции Грина и методы Фурье.

Это также особый вырожденный случай уравнения телеграфа, где индуктивность $L\; \{\backslash \; displaystyle\; L\}$исчезает, а скорость распространения сигнала $1\; /\; LC\; \{\backslash \; displaystyle\; 1\; /\; \{\backslash \; sqrt\; \{LC\}\}\}$бесконечно.

• Аксон
• Модель бидомена
• Биоэлектрохимия
• Модель биологического нейрона
• Дендрит
• Модель Ходжкина – Хаксли
• Мембранный потенциал
• Модель монодомена
• Уравнение Нернста – Планка
• Патч-зажим
• Сальтаторная проводимость
• Солитонная модель в нейробиологии

• Познанский, Роман Р. (2013). Математическая неврология. Сан-Диего [Калифорния]: Academic Press.
• Таквелл, Генри К. (1988). Введение в теоретическую нейробиологию. Кембридж [Кембриджшир]: Издательство Кембриджского университета. ISBN 978-0521350969.
• де Но, Рафаэль Лоренте (1947). Исследование физиологии нервов. Исследования Института медицинских исследований Рокфеллера. Отпечатки. Институт медицинских исследований Рокфеллера. стр. Часть I, 131: 1-496, Часть II, 132: 1-548. ISBN 9780598674722. OCLC 6217290.
• Лазаревич, Иван А.; Казанцев, Виктор Б. (2013). «Переход дендритного сигнала, вызванный внутриклеточным зарядом в неоднородностях». Phys. Ред. E. 88 (6): 062718. arXiv : 1308.0821. Bibcode : 2013PhRvE..88f2718L. doi : 10.1103 / PhysRevE.88.062718. PMID 24483497. S2CID 13353454.