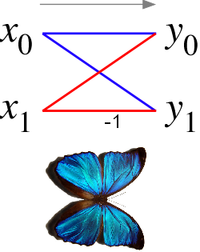Схема бабочки

Граф потока сигналов, соединяющий входы x (слева) с выходами y, которые зависят от них (справа) для шага «бабочка» БПФ Кули – Тьюки с основанием 2. Эта диаграмма напоминает бабочку (как в морфо-бабочке, показанном для сравнения), отсюда и название, хотя в некоторых странах ее также называют диаграммой песочных часов.

В контексте алгоритмов быстрого преобразования Фурье, бабочка - это часть вычисления, которая объединяет результаты меньшего дискретного преобразования Фурье (ДПФ) в большее ДПФ, или наоборот (разбиение большего ДПФ на частичные преобразования). Название «бабочка» происходит от формы диаграммы потока данных в случае radix-2, как описано ниже. Считается, что самым ранним появлением этого термина в печати является технический отчет 1969 MIT. Такую же структуру можно найти в алгоритме Витерби, который используется для поиска наиболее вероятной последовательности скрытых состояний.

Чаще всего термин «бабочка» появляется в контексте алгоритма БПФ Кули – Тьюки, который рекурсивно разбивает ДПФ составного размер n = rm в r меньших преобразований размера m, где r - "основание" преобразования. Эти более мелкие ДПФ затем объединяются с помощью бабочек размера r, которые сами являются ДПФ размера r (выполняются m раз на соответствующих выходных данных суб-преобразований), предварительно умноженные на корни из единицы (известные как факторы поворота ). (Это случай «прореживания во времени»; можно также выполнить шаги в обратном порядке, известные как «прореживание по частоте», когда сначала появляются бабочки, а затем умножаются на множители твиддла. См. Также Кули– Статья по БПФ Тьюки.)

Содержание

• 1 Диаграмма «бабочка» с основанием Radix-2
• 2 Другое использование
• 3 См. Также
• 4 Ссылки
• 5 Внешние ссылки

Radix-2 диаграмма бабочки

В случае алгоритма Кули – Тьюки с основанием 2, бабочка - это просто ДПФ размера 2, которое принимает два входа (x 0, x 1) (соответствующие выходные данные двух суб-преобразований) и дает два выходных сигнала (y 0, y 1) по формуле (не включая множителей тиддла ):

$y\; 0\; =\; x\; 0\; +\; x\; 1\; \{\backslash \; displaystyle\; y\_\; \{0\}\; =\; x\_\; \{0\}\; +\; x\_\; \{1\}\; \backslash ,\}$

$y\; 1\; =\; x\; 0\; -\; x\; 1.\; \{\backslash \; displaystyle\; y\_\; \{1\}\; =\; x\_\; \{0\}\; -x\_\; \{1\}.\; \backslash ,\}$

Если нарисовать диаграмму потока данных для этой пары операций, (x 0, x Линии от 1) до (y 0, y 1) пересекаются и напоминают крылья бабочки, отсюда и название (см. Также иллюстрацию справа).

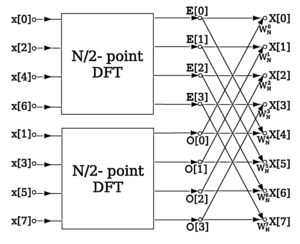БПФ с децимацией во времени по основанию 2 разбивает ДПФ длиной N на два ДПФ с длиной N / 2, за которыми следует этап комбинирования, состоящий из множества операций бабочки.

Более конкретно, прореживание по основанию 2 - своевременный алгоритм БПФ на n = 2 входах относительно примитивного корня n-й степени из единицы $\omega \; nk\; =\; e\; -\; 2\; \pi \; ikn\; \{\backslash \; displaystyle\; \backslash \; omega\; \_\; \{n\}\; ^\; \{k\}\; =\; e\; ^\; \{-\; \{\backslash \; frac\; \{2\; \backslash \; pi\; ik\}\; \{n\}\}\}\}$полагается на O (n log 2 n) бабочек в форме:

$y\; 0\; =\; x\; 0\; +\; Икс\; 1\; \omega \; NK\; \{\backslash \; Displaystyle\; Y\_\; \{0\}\; =\; X\_\; \{0\}\; +\; X\_\; \{1\}\; \backslash \; omega\; \_\; \{n\}\; ^\; \{k\}\; \backslash ,\}$

$y\; 1\; =\; x\; 0\; -\; x\; 1\; \omega \; nk,\; \{\backslash \; displaystyle\; y\_\; \{1\}\; =\; x\_\; \{0\}\; -x\_\; \{1\}\; \backslash \; omega\; \_\; \{n\}\; ^\; \{k\},\; \backslash ,\}$

, где k - целое число, зависящее от вычисляемой части преобразования. В то время как соответствующее обратное преобразование может быть выполнено математически путем замены ω на ω (и, возможно, умножения на общий масштабный коэффициент, в зависимости от соглашения о нормализации), можно также напрямую инвертировать бабочек:

$x\; 0\; =\; 1\; 2\; (y\; 0\; +\; y\; 1)\; \{\backslash \; displaystyle\; x\_\; \{0\}\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; (y\_\; \{0\}\; +\; y\_\; \{1\})\; \backslash ,\}$

$x\; 1\; =\; \omega \; n\; -\; k\; 2\; (y\; 0\; -\; y\; 1),\; \{\backslash \; displaystyle\; x\_\; \{1\}\; =\; \{\backslash \; frac\; \{\backslash \; omega\; \_\; \{n\}\; ^\; \{-\; k\}\}\; \{2\}\}\; (y\_\; \{0\}\; -y\_\; \{1\}),\; \backslash ,\}$

соответствующий алгоритму БПФ с децимацией по частоте.

Другое применение

Бабочка также может использоваться для улучшения случайности больших массивов частично случайных чисел, приводя каждое 32- или 64-битное слово в причинный контакт с каждым другим словом через желаемое алгоритм хеширования, так что изменение любого одного бита имеет возможность изменить все биты в большом массиве.

См. также

• Математическая диаграмма
• лемма Цассенхауза
• граф потока сигналов

Ссылки

1. ^Алан В. Оппенгейм, Рональд В. Шафер и Джон Р. Бак, Обработка сигналов в дискретном времени, 2-е издание (Верхняя Сэдл-Ривер, Нью-Джерси: Прентис-Холл, 1989)
2. ^С. Дж. Вайнштейн (1969-11-21). Эффекты квантования в цифровых фильтрах (Отчет). Лаборатория Линкольна Массачусетского технологического института. п. 42. Проверено 10 февраля 2015. Это вычисление называется «бабочкой»
3. ^Cipra, Barry A. (2012-06-04). «Диаграмма БПФ и бабочки». mathoverflow.net. Проверено 10 февраля 2015 г.
4. ^*Press, WH; Теукольский С.А.; Феттерлинг, штат Вашингтон; Фланнери, Б.П. (2007), «Раздел 7.2 Полное хеширование большого массива», Численные рецепты: Искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521-88068-8

Внешние ссылки

• объяснение диаграмм БПФ и бабочек.
• диаграмм бабочек различных реализаций БПФ (Radix-2, Radix-4, Split-Radix).