Линейный алгоритм Брезенхема

Алгоритм линии Брезенхема - это алгоритм рисования линии, который определяет точки n- мерного растра, которые должны быть выбраны, чтобы сформировать близкое приближение к прямой линии между двумя точками. Он обычно используется для рисования примитивов линий в растровом изображении (например, на экране компьютера ), так как он использует только целочисленное сложение, вычитание и сдвиг битов, все из которых являются очень дешевыми операциями в стандартных компьютерных архитектурах. Это алгоритм возрастающей ошибки. Это один из самых ранних алгоритмов, разработанных в области компьютерной графики. Для рисования кругов можно использовать расширение исходного алгоритма.

Хотя такие алгоритмы, как алгоритм Ву, также часто используются в современной компьютерной графике, поскольку они могут поддерживать сглаживание, скорость и простота линейного алгоритма Брезенхэма означает, что он по-прежнему важен. Алгоритм используется в оборудовании, таком как плоттеры, и в графических чипах современных видеокарт. Его также можно найти во многих графических библиотеках программного обеспечения. Поскольку алгоритм очень прост, он часто реализуется либо в прошивке, либо в графическом оборудовании современных видеокарт.

Обозначение «Брезенхэм» сегодня используется для семейства алгоритмов, расширяющих или изменяющих исходный алгоритм Брезенхема.

• 1 История
• 2 Метод
• 3 Вывод
  • 3.1 Уравнение линии
  • 3.2 Алгоритм
    • 3.2.1 Алгоритм целочисленной арифметики
  • 3.3 Все случаи
• 4 Подобные алгоритмы
• 5 См. Также
• 6 Примечания
• 7 ссылки
• 8 Дальнейшее чтение
• 9 Внешние ссылки

Линейный алгоритм Брезенхема назван в честь Джека Элтона Брезенхема, который разработал его в 1962 году в IBM. В 2001 году Брезенхэм писал:

Я работал в вычислительной лаборатории лаборатории разработки IBM в Сан-Хосе. Calcomp плоттер был прикреплен к IBM 1401 через консоль 1407 пишущей машинки. [Алгоритм] использовался в производстве летом 1962 года, возможно, на месяц или около того раньше. В те дни корпорации свободно обменивались программами, поэтому у Calcomp (Джим Ньюленд и Кэлвин Хефте) были копии. Когда я вернулся в Стэнфорд осенью 1962 года, я положил копию в библиотеку Стэнфордского вычислительного центра. Описание процедуры рисования линий было принято для презентации на национальном съезде ACM 1963 года в Денвере, штат Колорадо. Это был год, в котором не было опубликовано никаких материалов, только повестка дня докладчиков и темы в выпуске сообщений ACM. После того, как я выступил с презентацией, человек из IBM Systems Journal спросил меня, могут ли они опубликовать статью. Я с радостью согласился, и они напечатали его в 1965 году.

Алгоритм Брезенхема был расширен для создания кругов, эллипсов, кубических и квадратичных кривых Безье, а также их собственных сглаженных версий.

Иллюстрация результата линейного алгоритма Брезенхема. (0,0) находится в верхнем левом углу сетки, (1,1) находится в верхнем левом конце строки, а (11, 5) находится в правом нижнем конце строки.

Будут использоваться следующие условные обозначения:

• верхний левый угол равен (0,0), так что координаты пикселей увеличиваются в направлениях вправо и вниз (например, пиксель в точке (7,4) находится непосредственно над пикселем в точке (7,5)), и
• центры пикселей имеют целочисленные координаты.

Конечные точки линии - это пиксели в и, где первая координата пары - это столбец, а вторая - строка. ${\ displaystyle (x_ {0}, y_ {0})}$${\ displaystyle (x_ {1}, y_ {1})}$

Изначально алгоритм будет представлен только для октанта, в котором сегмент идет вниз и вправо ( и), а его горизонтальная проекция длиннее вертикальной проекции (линия имеет положительный наклон меньше 1). В этом октанте для каждого столбца x между и существует ровно одна строка y (вычисленная алгоритмом), содержащая пиксель строки, в то время как каждая строка между и может содержать несколько растеризованных пикселей. ${\ Displaystyle x_ {0} \ leq x_ {1}}$${\ displaystyle y_ {0} \ leq y_ {1}}$${\ displaystyle x_ {1} -x_ {0}}$${\ displaystyle y_ {1} -y_ {0}}$ ${\ displaystyle x_ {0}}$${\ displaystyle x_ {1}}$${\ displaystyle y_ {0}}$${\ displaystyle y_ {1}}$

Алгоритм Брезенхема выбирает целое число y, соответствующее центру пикселя, которое наиболее близко к идеальному (дробному) y для того же x ; в следующих друг за другом столбцах y может оставаться неизменным или увеличиваться на 1. Общее уравнение линии, проходящей через конечные точки, определяется следующим образом:

${\ displaystyle {\ frac {y-y_ {0}} {y_ {1} -y_ {0}}} = {\ frac {x-x_ {0}} {x_ {1} -x_ {0}}} }$.

Поскольку мы знаем столбец x, строка пикселя y задается округлением этой величины до ближайшего целого числа:

${\ displaystyle y = {\ frac {y_ {1} -y_ {0}} {x_ {1} -x_ {0}}} (x-x_ {0}) + y_ {0}}$.

Наклон зависит только от координат конечной точки и может быть вычислен заранее, а идеальный y для последовательных целочисленных значений x может быть вычислен, начиная с многократного добавления наклона. ${\ displaystyle (y_ {1} -y_ {0}) / (x_ {1} -x_ {0})}$${\ displaystyle y_ {0}}$

На практике алгоритм не отслеживает координату y, которая увеличивается на m = ∆y / ∆x каждый раз, когда x увеличивается на единицу; он сохраняет границу ошибки на каждом этапе, которая представляет собой отрицательное значение расстояния от (а) точки, где линия выходит из пикселя, до (b) верхнего края пикселя. Это значение сначала устанавливается на (из-за использования координат центра пикселя) и увеличивается на m каждый раз, когда координата x увеличивается на единицу. Если ошибка становится больше 0,5, мы знаем, что линия переместилась вверх на один пиксель, и что мы должны увеличить нашу координату y и скорректировать ошибку, чтобы представить расстояние от вершины нового пикселя, что выполняется путем вычитания единицы из ошибка. ${\ displaystyle y_ {0} -0,5}$

Чтобы вывести алгоритм Брезенхема, необходимо сделать два шага. Первым шагом является преобразование уравнения линии из типичной формы пересечения наклона во что-то другое; а затем с помощью этого нового уравнения провести линию, основанную на идее накопления ошибок.

Уравнение линии

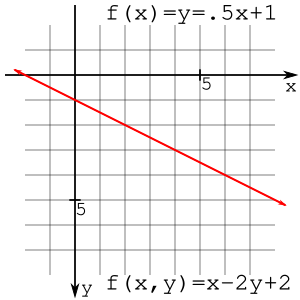y = f (x) =. 5x + 1 или f (x, y) = x-2y + 2 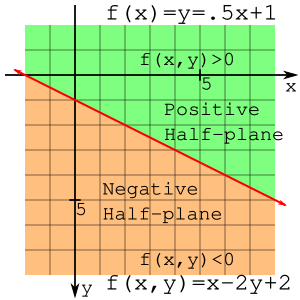Положительные и отрицательные полуплоскости

Форма линии с пересечением наклона записывается как

${\ Displaystyle у = е (х) = mx + b}$

где m - наклон, а b - точка пересечения с y. Это функция только от x, и было бы полезно записать это уравнение как функцию от x и y. Используя алгебраические манипуляции и распознавая, что уклон - это "подъем через пробег", или затем ${\ displaystyle \ Delta y / \ Delta x}$

${\ displaystyle {\ begin {align} y amp; = mx + b \\ y amp; = {\ frac {(\ Delta y)} {(\ Delta x)}} x + b \\ (\ Delta x) y amp; = (\ Delta y) x + (\ Delta x) b \\ 0 amp; = (\ Delta y) x - (\ Delta x) y + (\ Delta x) b \ end {выровнено}}}$

Если это последнее уравнение является функцией x и y, то его можно записать как

${\ displaystyle f (x, y) = 0 = Ax + By + C}$

где постоянные

• ${\ displaystyle A = \ Delta y}$
• ${\ displaystyle B = - \ Delta x}$
• ${\ Displaystyle C = (\ Delta x) b}$

Затем линия определяется для некоторых констант A, B и C где угодно. Тогда для любого, кто не на кону. Все в этой форме включает только целые числа, если x и y являются целыми числами, поскольку константы обязательно являются целыми числами. ${\ displaystyle f (x, y) = 0}$${\ Displaystyle (х, у)}$${\ Displaystyle е (х, у) \ neq 0}$

Например, строка this может быть записана как. Точка (2,2) находится на прямой ${\ Displaystyle у = {\ гидроразрыва {1} {2}} х + 1}$${\ Displaystyle е (х, у) = х-2у + 2}$

${\ Displaystyle f (2,2) = x-2y + 2 = (2) -2 (2) + 2 = 2-4 + 2 = 0}$

и точка (2,3) не находится на прямой

${\ Displaystyle f (2,3) = (2) -2 (3) + 2 = 2-6 + 2 = -2}$

и ни точка (2,1)

${\ Displaystyle f (2,1) = (2) -2 (1) + 2 = 2-2 + 2 = 2}$

Обратите внимание, что точки (2,1) и (2,3) находятся на противоположных сторонах линии, и f (x, y) оценивается как положительное или отрицательное. Линия разделяет плоскость пополам, и полуплоскость с отрицательным f (x, y) может быть названа отрицательной полуплоскостью, а другая половина - положительной полуплоскостью. Это наблюдение очень важно для оставшейся части вывода.

Алгоритм

Ясно, что отправная точка находится на прямой

${\ displaystyle f (x_ {0}, y_ {0}) = 0}$

только потому, что линия определена так, чтобы начинаться и заканчиваться в целочисленных координатах (хотя вполне разумно захотеть нарисовать линию с нецелочисленными конечными точками).

Кандидатские баллы (2,2) отмечены синим цветом, а два кандидатских балла - зеленым (3,2) и (3,3).

Принимая во внимание, что наклон меньше или равен единице, теперь возникает проблема: должна ли следующая точка находиться в точке или. Возможно, интуитивно следует выбирать точку, исходя из того, какая точка находится ближе к линии. Если он ближе к первому, включите первую точку на линии, если второй, то второй. Чтобы ответить на этот вопрос, оцените функцию линии в середине между этими двумя точками: ${\ displaystyle (x_ {0} + 1, y_ {0})}$${\ displaystyle (x_ {0} + 1, y_ {0} +1)}$${\ displaystyle x_ {0} +1}$

${\ displaystyle f (x_ {0} + 1, y_ {0} + {\ tfrac {1} {2}})}$

Если значение этого параметра положительное, то идеальная линия находится ниже средней точки и ближе к точке-кандидату ; в действительности координата y продвинулась вперед. В противном случае идеальная линия проходит через или выше средней точки, а координата y не продвигается; в этом случае выберите точку. Это наблюдение очень важно понять! Значение линейной функции в этой средней точке является единственным определяющим фактором, какую точку следует выбрать. ${\ displaystyle (x_ {0} + 1, y_ {0} +1)}$${\ displaystyle (x_ {0} + 1, y_ {0})}$

На соседнем изображении показана синяя точка (2,2), выбранная для расположения на линии с двумя точками-кандидатами зеленого цвета (3,2) и (3,3). Черная точка (3, 2.5) - это середина между двумя точками-кандидатами.

Алгоритм целочисленной арифметики

В качестве альтернативы можно использовать разницу между точками вместо оценки f (x, y) в средних точках. Этот альтернативный метод позволяет выполнять арифметику только с целыми числами, что обычно быстрее, чем использование арифметики с плавающей запятой. Чтобы получить альтернативный метод, определите разницу следующим образом:

${\ displaystyle D = f (x_ {0} + 1, y_ {0} + {\ tfrac {1} {2}}) - f (x_ {0}, y_ {0})}$

Для первого решения эта формулировка эквивалентна методу средней точки, так как в начальной точке. Упрощение этого выражения дает: ${\ displaystyle f (x_ {0}, y_ {0}) = 0}$

${\ displaystyle {\ begin {array} {rclcl} D amp; = amp; \ left [A (x_ {0} +1) + B \ left (y_ {0} + {\ frac {1} {2}} \ right) + C \ right] amp; - amp; \ left [Ax_ {0} + By_ {0} + C \ right] \\ amp; = amp; \ left [Ax_ {0} + By_ {0} + C + A + {\ frac { 1} {2}} B \ right] amp; - amp; \ left [Ax_ {0} + By_ {0} + C \ right] \\ amp; = amp; A + {\ frac {1} {2}} B \ end {массив }}}$

Как и в случае с методом средней точки, если D положительно, выберите, в противном случае выберите. ${\ displaystyle (x_ {0} + 1, y_ {0} +1)}$${\ displaystyle (x_ {0} + 1, y_ {0})}$

Если выбрано, изменение D будет: ${\ displaystyle (x_ {0} + 1, y_ {0})}$

${\ displaystyle {\ begin {array} {lclcl} \ Delta D amp; = amp; f (x_ {0} + 2, y_ {0} + {\ tfrac {1} {2}}) - f (x_ {0} +1, y_ {0} + {\ tfrac {1} {2}}) amp; = amp; A amp; = amp; \ Delta y \\\ end {array}}}$

Если выбрано, изменение D будет: ${\ displaystyle (x_ {0} + 1, y_ {0} +1)}$

${\ displaystyle {\ begin {array} {lclcl} \ Delta D amp; = amp; f (x_ {0} + 2, y_ {0} + {\ tfrac {3} {2}}) - f (x_ {0} +1, y_ {0} + {\ tfrac {1} {2}}) amp; = amp; A + B amp; = amp; \ Delta y- \ Delta x \ end {array}}}$

Если новый D положительный, то выбирается, в противном случае. Это решение можно обобщить, накапливая ошибку в каждой последующей точке. ${\ displaystyle (x_ {0} + 2, y_ {0} +1)}$${\ displaystyle (x_ {0} + 2, y_ {0})}$

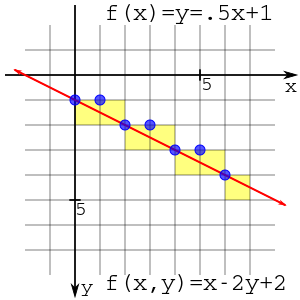Построение линии от (0,1) до (6,4), показывающее график линий сетки и пикселей

Весь вывод алгоритма сделан. Одной из проблем производительности является коэффициент 1/2 в начальном значении D. Поскольку все это относится к знаку накопленной разницы, тогда все можно умножить на 2 без каких-либо последствий.

В результате получается алгоритм, использующий только целочисленную арифметику.

plotLine(x0, y0, x1, y1) dx = x1 - x0 dy = y1 - y0 D = 2*dy - dx y = y0 for x from x0 to x1 plot(x,y) if D gt; 0 y = y + 1 D = D - 2*dx end if D = D + 2*dy

Выполнение этого алгоритма для от (0,1) до (6,4) дает следующие различия с dx = 6 и dy = 3: ${\ Displaystyle е (х, у) = х-2у + 2}$

D=2*3-6=0 Loop from 0 to 6 * x=0: plot(0, 1), D≤0: D=0+6=6 * x=1: plot(1, 1), Dgt;0: D=6-12=-6, y=1+1=2, D=-6+6=0 * x=2: plot(2, 2), D≤0: D=0+6=6 * x=3: plot(3, 2), Dgt;0: D=6-12=-6, y=2+1=3, D=-6+6=0 * x=4: plot(4, 3), D≤0: D=0+6=6 * x=5: plot(5, 3), Dgt;0: D=6-12=-6, y=3+1=4, D=-6+6=0 * x=6: plot(6, 4), D≤0: D=0+6=6

Результат этого графика показан справа. Построение можно просмотреть, вычерчивая на пересечении линий (синие кружки) или заполняя пиксельные поля (желтые квадраты). Тем не менее, сюжет такой же.

Все кейсы

Однако, как упоминалось выше, это только для нулевого октанта, то есть линий, начинающихся в начале координат с градиентом между 0 и 1, где x увеличивается ровно на 1 за итерацию, а y увеличивается на 0 или 1.

Алгоритм может быть расширен для охвата градиентов от 0 до -1, проверяя, нужно ли y увеличивать или уменьшать (т.е. dy lt;0)

plotLineLow(x0, y0, x1, y1) dx = x1 - x0 dy = y1 - y0 yi = 1 if dy lt; 0 yi = -1 dy = -dy end if D = (2 * dy) - dx y = y0 for x from x0 to x1 plot(x, y) if D gt; 0 y = y + yi D = D + (2 * (dy - dx)) else D = D + 2*dy end if

Путем переключения осей x и y реализация для положительных или отрицательных крутых градиентов может быть записана как

plotLineHigh(x0, y0, x1, y1) dx = x1 - x0 dy = y1 - y0 xi = 1 if dx lt; 0 xi = -1 dx = -dx end if D = (2 * dx) - dy x = x0 for y from y0 to y1 plot(x, y) if D gt; 0 x = x + xi D = D + (2 * (dx - dy)) else D = D + 2*dx end if

Полное решение должно было бы определить, x1gt; x0 или y1gt; y0 и поменять местами входные координаты перед рисованием, таким образом

plotLine(x0, y0, x1, y1) if abs(y1 - y0) lt; abs(x1 - x0) if x0 gt; x1 plotLineLow(x1, y1, x0, y0) else plotLineLow(x0, y0, x1, y1) end if else if y0 gt; y1 plotLineHigh(x1, y1, x0, y0) else plotLineHigh(x0, y0, x1, y1) end if end if

В низкоуровневых реализациях, которые обращаются к видеопамяти напрямую, было бы типично, чтобы особые случаи вертикальных и горизонтальных линий обрабатывались отдельно, поскольку они могут быть сильно оптимизированы.

Некоторые версии используют принципы Брезенхема целочисленной инкрементной ошибки для выполнения всех рисований линий октанта, уравновешивая положительную и отрицательную ошибку между координатами x и y. Обратите внимание, что порядок не обязательно гарантирован; другими словами, линия может быть проведена от (x0, y0) до (x1, y1) или от (x1, y1) до (x0, y0).

plotLine(int x0, int y0, int x1, int y1) dx = abs(x1-x0); sx = x0lt;x1 ? 1 : -1; dy = -abs(y1-y0); sy = y0lt;y1 ? 1 : -1; err = dx+dy; /* error value e_xy */ while (true) /* loop */ plot(x0, y0); if (x0 == x1 amp;amp; y0 == y1) break; e2 = 2*err; if (e2 gt;= dy) /* e_xy+e_x gt; 0 */ err += dy; x0 += sx; end if if (e2 lt;= dx) /* e_xy+e_y lt; 0 */ err += dx; y0 += sy; end if end while

Алгоритм Брезенхема можно интерпретировать как слегка модифицированный цифровой дифференциальный анализатор (с использованием 0,5 в качестве порога ошибки вместо 0, который требуется для растеризации неперекрывающихся полигонов).

Принцип использования инкрементной ошибки вместо операций деления имеет и другие приложения в графике. Этот метод можно использовать для вычисления координат U, V во время растрового сканирования полигонов с отображением текстуры. В вокселей двигатели программного обеспечения визуализации HeightMap видел в некоторых компьютерных играх также использовали этот принцип.

Брезенхэм также опубликовал вычислительный алгоритм Run-Slice (в отличие от Run-Length). Этот метод был представлен в ряде патентов США:

5 815 163		Способ и устройство для рисования срезов линий во время расчета
5 740 345		Способ и устройство для отображения данных компьютерной графики, хранящихся в сжатом формате, с эффективной системой индексации цветов.
5 657 435		Запуск механизма рисования линий среза с возможностями нелинейного масштабирования
5 627 957		Механизм рисования линий среза с расширенными возможностями обработки
5 627 956		Механизм рисования линий среза с возможностью растягивания
5 617 524		Запуск механизма рисования линий среза с возможностью затенения
5 611 029		Запуск механизма рисования линий среза с возможностями нелинейного затенения
5 604 852		Способ и устройство для отображения параметрической кривой на видеодисплее
5 600 769		Запуск механизма рисования линий среза с улучшенными методами отсечения

Расширение алгоритма, обрабатывающего толстые линии, было создано Аланом Мерфи из IBM.

• Цифровой дифференциальный анализатор (графический алгоритм), простой и общий метод растеризации линий и треугольников
• Линейный алгоритм Xiaolin Wu, аналогичный быстрый метод рисования линий со сглаживанием
• Алгоритм средней точки круга, аналогичный алгоритм для рисования кругов

• Брезенхэм, Дж. Э. (1965). «Алгоритм компьютерного управления цифровым плоттером» (PDF). IBM Systems Journal. 4 (1): 25–30. DOI : 10.1147 / sj.41.0025. Архивировано из оригинального (PDF) 28 мая 2008 года.
• "Алгоритм рисования линий Брезенхема", Колин Фланаган
• Абраш, Майкл (1997). Черная книга Майкла Абраша по графическому программированию. Олбани, штат Нью-Йорк: Кориолис. С.  654–678. ISBN   978-1-57610-174-2. Очень оптимизированная версия алгоритма на C и сборка для использования в видеоиграх с полными деталями его внутренней работы.
• Зингл, Алоис (2012). «Алгоритм растеризации для построения кривых» (PDF)., Красота алгоритмов Брезенхема

• Тезис Патрика-Жиля Майо является расширением алгоритма рисования линий Брезенхэма для выполнения удаления скрытых трехмерных линий; также опубликовано в трудах MICAD '87 по CAD / CAM и компьютерной графике, стр. 591 - ISBN   2-86601-084-1.
• Утолщение линии путем модификации алгоритма Брезенхема, А.С. Мерфи, Технический бюллетень IBM, Vol. 20, No. 12, май 1978 г.

вместо [which] для использования расширения круга: Технический отчет 1964, 27 января -11- Алгоритм круга TR-02-286 Лаборатория IBM в Сан-Хосе или линейный алгоритм для инкрементального цифрового отображения круговых дуг, февраль 1977 г. Связь с ACM 20 (2): 100-106 DOI: 10.1145 / 359423.359432

• Черная книга Майкла Абраша по графическому программированию, специальное издание: Глава 35: Брезенхэм быстр, а быстр - хорош
• Алгоритм рисования линий Брезенхема Колина Фланагана
• Страница Национального института стандартов и технологий по алгоритму Брезенхема
• Информация о инкрементальном плоттере Calcomp 563
• Алгоритм Брезенхема на нескольких языках программирования
• Красота алгоритма Брезенхема - простая реализация для построения линий, кругов, эллипсов и кривых Безье