Модель Бора

Модель атома, представленная Нильсом Бором в 1913 г. Модель пирога атома водорода (Z = 1) или водородоподобный ион (Z>1), где отрицательно заряженный электрон, ограниченный атомной оболочкой, окружает небольшое положительно заряженное атомное ядро ​​ и когда электрон прыгает между орбитами, это сопровождается испускаемой или поглощенной величиной электромагнитной энергией (hν). Орбиты, по которому может перемещаться электрон, показаны серыми кружками; их радиус как увеличить n, где n - главное квантовое число . Выполненный здесь переход 3 → 2 дает первую строку серии Бальзам для воды (Z = 1) дает фотон с длиной волны 656 нм (красный свет).

В атомной физике, модель Бора или модель Резерфорда - Бора, представленная Нильсом Бором и Эрнест Резерфорд в 1913 году, представляет собой систему, состоящую из небольшого плотного ядра, окруженного вращающимися электронами, аналогичную структуру Солнечной системы, но с притяжением, защищенным электростатические силы вместо силы тяжести. После кубической модели (1902), модели сливового пудинга (1904), модели Сатурна (1904) и модели Резерфорда (1911 г.) появилась модель Резерфорда - Бора или просто модель Бора для краткости (1913 г.). Улучшение модели Резерфорда - это в основном ее квантовая физическая интерпретация. Ключевой успех модели заключался в объяснении формулы Ридберга для спектральных эмиссионных линий атомарного водорода. Хотя формула Ридберга была известна экспериментально, она не получила теоретического обоснования до тех пор, пока не представлена ​​модель Бора. Модель Бора не только объясняла причины формулы Ридберга, но необходимо обоснование фундаментальных физических констант, составляющих эмпирические результаты формулы.

Модель Бора является относительно примитивной моделью атома водорода по сравнению с моделью атома валентной оболочки. Теоретически его можно вывести как приближение первого порядка атома с использованием более широкой и гораздо более точной квантовой механики и таким образом, можно рассматривать как устаревшая научная теория. Однако из-за своей простоты и правильных результатов для выбранных систем (см. Приложение ниже), модель Бора все еще обычно преподают для ознакомления студентов с квантовой механикой или диаграммами уровней энергии прежде чем перейти к более точному, но более сложному атому валентной оболочки. Родственная модель была предложена Артуром Эрихом Хаасом в 1910 году, но была отклонена. Квантовая теория периода между открытием Планком квантовой (1900) и появлением зрелой квантовой механики (1925) часто упоминается как старая квантовая теория..

Содержание

• 1 Происхождение
• 2 Уровни энергии электронов
  • 2.1 Вывод
• 3 Формула Ридберга
• 4 Модель оболочки (более тяжелые атомы)
• 5 Закон и расчет Мозли (K-alpha X линии излучения)
• 6 Недостатки
• 7 Уточнения
• 8 Модель химической связи
• 9 См. также
• 10 Ссылки
  • 10.1 Сноски
  • 10.2 Первичные источники
• 11 Дополнительная литература
• 12 Внешние ссылки

Происхождение

Модель Бора, показывающая максимальное количество электронов на одну оболочку с оболочками, соответствующими в рентгеновской нотации

В начале 20-го века эксперименты Эрнеста Резерфорда установлено, что атомы состоят из диффузного облака отрицательно заряженных электронов, окружающего небольшое плотное положительно заряженное ядро ​​. Эти экспериментальные данные рассматривают планетарную модель атома, модель Резерфорда 1911 года - электроны вращаются вокруг ядра Солнца - однако данная планетарная модель атома имеет техническую трудность: законы Классическая механика (т.е. формула Лармора ) предсказывает, что электрон испустит электромагнитное излучение, вращаясь вокруг ядра. Он быстро движется по спирали внутрь, коллапсируя в ядро ​​за время около 16 пикосекунд. Эта модель атома катастрофична, потому что она предсказывает, что все атомы нестабильны.

Кроме того, по мере того, как электрон вращается внутри, частота вращения увеличивается по мере того, как орбита становится меньше и быстрее. Это привело бы к непрерывному размытию по частоте электромагнитного излучения. Однако эксперименты конца 19 века с электрическими разрядами показали, что атомы излучают свет (то есть электромагнитное излучение) только на определенных дискретных частотах.

Чтобы преодолеть эту трудную трудность, Нильс Бор в 1913 году то, что сейчас называется моделью атома Бора. Он выдвинул эти три большой постулата, которые суммируют часть модели:

1. Электрон может вращаться по определенным стабильным орбитам вокруг ядра, не излучая никакой энергии, в отличие от того, что предлагает классический электромагнетизм. Эти стабильные орбиты называются стационарными орбитами и достигаются на определенных расстояниях от ядра. Электрон не может иметь никакой другой орбиты между дискретными.
2. Стационарные орбиты достигаются на расстояниях, на которых вращается вращающегося электрода является целым кратным приведенной Планка : $mevr\; =\; n\; \hslash \; \{\backslash \; displaystyle\; m\; \_\; \{\backslash \; mathrm\; \{e\}\}\; vr\; =\; n\; \backslash \; hbar\}$, где n = 1, 2, 3,... называется главное квантовое число и ħ = h / 2π. Наименьшее значение n равно 1; это дает наименьший возможный радиус орбиты 0,0529 нм, известный как радиус Бора. Когда электрон оказывается на этой нижней орбите, он не может приблизиться к протону. Исходя из квантового правила углового момента, Бор смог вычислить энергии разрешенных орбит атома водорода и других водородоподобных элементов и оригина. Эти орбиты связаны с определенными энергиями и также называются энергетическими оболочками или уровнями энергии. На этих орбитах ускорение электрона не приводит к потере излучения и энергии. Модель атома Бора была на квантовой теории излучения Планка.
3. Электроны могут набирать и терять энергию, только прыгая с одной разрешенной орбиты на другую, поглощенную или испуская электромагнитное излучение с параметром ν, определяемой энергией разности уровней использованию Планка : $\Delta \; E\; =\; E\; 2\; -\; E\; 1\; =\; h\; \nu \; \{\backslash \; displaystyle\; \backslash \; Delta\; E\; =\; E\_\; \{2\}\; -E\_\; \{1\}\; =\; h\; \backslash \; nu\}$, где h - постоянная Планка.

Другие моменты :

1. Как и теория Эйнштейна о фотоэлектрический эффект, формула Бора предполагает, что во время квантового скачка дискретное количество энергии излучается. Однако, в отличие от Эйнштейна, Борьба с классической теории Максвелла электромагнитного поля. Квантование электромагнитного поля объяснялось дискретностью атомных энергетических уровней ; Бор не верил в существование фотонов.
2. Согласно теории Максвелла частота ν классического этого частоты вращения ν rot электрона на его орбите, причем гармоники, кратные частоты. Этот результат получается из моделей Бора для скачков между уровнями энергии E n и E n-k, когда k намного меньше n. Эти скачки воспроизводят частоту k-й гармоники орбиты n. Для достаточно больших значений n (так называемые состояния Ридберга ) две орбиты, участвующие в процессе излучения, имеют почти одинаковую частоту вращения, так что классическая орбитальная частота не является неоднозначной. Но при малых n (или больших k) частота излучения не имеет однозначной классической интерпретации. Это знаменует рождение принцип соответствия, требуемого согласования квантовой теории с классической теорией только в пределе больших квантовых чисел.
3. Теория Бора - Крамерса - Слейтера (теория BKS) - это неудачная попытка расширить модель Бора, которая нарушает сохранение энергии и импульса в квантовых скачках, при этом сохранении выполняются только в среднем.

Условие Бора о том, что угловой момент является целым числом, кратным ħ, было позже переинтерпретировано в 1924 году де Бройлем как условие стоячей волны : описывается волной и целое число длин должно соответствовать окружности орбиты электрона:

$n\; \lambda \; =\; 2\; \pi \; r.\; \{\backslash \; displaystyle\; n\; \backslash \; lambda\; =\; 2\; \backslash \; pi\; r.\}$

Согласно гипотезе де Бройля, частицы материи, такие как электрон, ведут себя как волны. Итак, длина волны электрона по де Бройлю равна:

$\lambda \; =\; hmv\; \{\backslash \; displaystyle\; \backslash \; lambda\; =\; \{\backslash \; frac\; \{h\}\; \{mv\}\}\}$.

, что означает,

$nhmv\; =\; 2\; \pi \; r\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{nh\}\; \{mv\}\}\; =\; 2\; \backslash \; pi\; r\}$

или

$nh\; 2\; \pi \; =\; mvr\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{nh\}\; \{2\; \backslash \; pi\}\}\; =\; mvr\}$

где $mvr\; \{\backslash \; displaystyle\; mvr\}$- угловой момент $\ell \; \{\backslash \; displaystyle\; \backslash \; ell\}$вращающегося электрона.

$\ell \; =\; n\; час\; 2\; \pi \; \{\backslash \; displaystyle\; \backslash \; ell\; =\; \{\backslash \; frac\; \{nh\}\; \{2\; \backslash \; pi\}\}\}$

, что является вторым постулатом Бора.

Бор описал угловой момент электронной орбиты как 1 / 2h, в то время как длина волны де Бройля λ = h / p описывала h, деленное на импульс электрона. Однако в 1913 году Борьба обосновал свое правило, апеллируя к принципу соответствия, не давая никакой интерпретации волн. В 1913 году о волновом поведении частиц материи, таких как электроны (т.е. волны материи ), не подозревали.

В 1925 году был предложен новый вид механики, квантовая механика, в которой модель Бора электронов, движущихся по квантованным орбитам, была расширена до более точной модели движение электронов. Новую теорию использования Вернер Гейзенберг. Другая форма той же теории, волновая механика, была открыта австрийским физиком Эрвином Шрёдингером независимо и по другим причинам. Шредингер использовал волны материи де Бройля, но искал волновые решения трехмерного волнового уравнения, которые были вынуждены двигаться вокруг ядра водородоподобного атома, будучи захваченными потенциалом положительного ядерный заряд.

Уровни энергии электронов

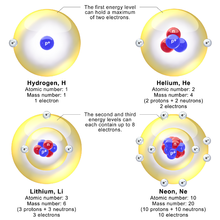Модели, демонстрирующие уровни энергии электронов в водороде, гелии, литии и неоне

Модель Бора дает почти точные результаты только для системы, в которой две заряженные точки вращаются друг вокруг друга со скоростью меньше, чем у света. Это касается не только одноэлектронных систем, таких как атом водорода, дважды ионизированный гелий и дважды ионизированный литий, но и позитроний и Ридберговские состояния любого атома, где один электрон находится далеко от всего остального. Его можно использовать для расчетов рентгеновских переходов K-линии, если добавлены другие допущения (см. закон Мозли ниже). В физике высоких энергий его можно использовать для расчета масс тяжелых кварков мезонов.

Для расчета орбит требуется два предположения.

• Классическая механика

Электрон удерживается на круговой орбите за счет электростатического притяжения. центростремительная сила равна кулоновской силе.

$mev\; 2\; r\; =\; Z\; kee\; 2\; r\; 2\; \{\backslash \; displaystyle\; \{m\; \_\; \{\backslash \; mathrm\; \{e\}\}\; v\; ^\; \{2\}\; \backslash \; over\; r\}\; =\; \{\; Zk\; \_\; \{\backslash \; mathrm\; \{e\}\}\; e\; ^\; \{2\}\; \backslash \; over\; r\; ^\; \{2\}\}\}$

где m e - масса электрона, e - заряд электрона, k e - кулоновская постоянная и Z - атомный номер атома. Ядро, что ядро ​​намного больше массы электрона. Это уравнение определяет скорость электрона на любом радиусе:

$v\; =\; Z\; k\; e\; e\; 2\; m\; e\; r.\; \{\backslash \; displaystyle\; v\; =\; \{\backslash \; sqrt\; \{Zk\; \_\; \{\backslash \; mathrm\; \{e\}\}\; e\; ^\; \{2\}\; \backslash \; over\; m\; \_\; \{\backslash \; mathrm\; \{e\}\}\; r\}\}.\}$

Он также определяет полную энергию электрона на любом радиусе:

$E\; =\; -\; 1\; 2\; мэв\; 2\; \{\backslash \; displaystyle\; E\; =\; -\; \{1\; \backslash \; over\; 2\}\; m\; \_\; \{\backslash \; mathrm\; \{e\}\}\; v\; ^\; \{2\}\}$

Полная энергия отрицательна и обратно пропорциональна r. Это означает, что требуется энергия, чтобы оттолкнуть вращающийся электрон от протона. Для бесконечных значений r энергия равна нулю, что соответствует неподвижному электрону, бесконечно удаленному от протона. Полная энергия составляет половину потенциальной энергии, разница составляет кинетическую энергию электрона. Это также верно для некруглых орбитов по теореме вириала.

• Квантовому правилу

угловой момент L = m e vr является целым кратным ħ:

$mevr\; =\; n\; \hslash \; \{\backslash \; displaystyle\; m\; \_\; \{\backslash \; mathrm\; \{e\}\}\; vr\; =\; n\; \backslash \; hbar\}$

Вывод

Если электрон в атоме движется по орбите с периодом T, классически электромагнитное излучение будет повторяться каждый период обращения. Если связь с электромагнитным полем слабая, так что орбита не сильно затухает за один цикл, излучение будет испускаться по схеме, которая повторяется каждый период, так что преобразование Фурье будет иметь частоты, которые только кратны 1 / Т. Это классический закон излучения: излучаемые частоты кратны 1 / T.

В квантовой механике это излучение должно происходить в квантах света с частотами, состоящими из целых кратных 1 / T, так что классическая механика является кратким описанием при больших квантовых числах. Это означает, что уровень энергии, соответствующий классической орбите с периодом 1 / T, должен иметь соседние энергетические уровни, которые различаются по энергии на h / T, и они должны быть равномерно распределены около этого уровня,

$\Delta \; E\; n\; =\; h\; T\; (Эн).\; \{\backslash \; displaystyle\; \backslash \; Delta\; E\_\; \{n\}\; =\; \{h\; \backslash \; over\; T\; (E\_\; \{n\})\}.\}$

Бороздился о том, следует ли лучше всего рассчитывать энергетический интервал 1 / T с периодом энергетического состояния $E\; n\; \{\backslash \; displaystyle\; E\_\; \{n\}\}$, или $E\; n\; +\; 1\; \{\backslash \; displaystyle\; E\_\; \{n\; +\; 1\}\}$, или какое-то среднее - в ретроспективе это модель является лишь ведущим полуклассическим приближением.

Бор считал круговые орбиты. Классически эти орбиты должны распадаться на меньшие круги при испускании фотонов. Расстояние между круговыми орбитами можно рассчитать по формуле соответствия. Для атома водорода классические орбиты имеют определяемый третьим законом Кеплера в масштабе г. Энергия масштабируется как 1 / r, поэтому формула расстояния между уровнями составляет

$\Delta \; E\; \propto \; 1\; r\; 3\; 2\; \propto \; E\; 3\; 2.\; \{\backslash \; displaystyle\; \backslash \; Delta\; E\; \backslash \; propto\; \{1\; \backslash \; over\; r\; ^\; \{3\; \backslash \; over\; 2\}\}\; \backslash \; propto\; E\; ^\; \{3\; \backslash \; over\; 2\}.\}$

Можно определить уровни энергии, рекурсивно пониженная орбиту на орбита, но есть ярлык.

Угловой момент L круговой орбиты масштабируется как √r. Энергия в единицах углового момента равна

$E\; \propto \; 1\; r\; \propto \; 1\; L\; 2\; \{\backslash \; displaystyle\; E\; \backslash \; propto\; \{1\; \backslash \; over\; r\}\; \backslash \; propto\; \{1\; \backslash \; over\; L\; ^\; \{2\}\}\}$.

Предполагая, согласно Бору, квантованные значения L равномерно распределены, расстояние между соседними энергиями

$\Delta \; E\; \propto \; 1\; (L\; +\; \hslash )\; 2\; -\; 1\; L\; 2\; \approx \; -\; 2\; \hslash \; L\; 3\; \propto \; -\; E\; 3\; 2.\; \{\backslash \; displaystyle\; \backslash \; Delta\; E\; \backslash \; propto\; \{1\; \backslash \; over\; (L\; +\; \backslash \; hbar)\; ^\; \{2\}\}\; -\; \{1\; \backslash \; over\; L\; ^\; \{2\}\}\; \backslash \; приблизительно\; -\; \{2\; \backslash \; hbar\; \backslash \; over\; L\; ^\; \{3\}\}\; \backslash \; propto\; -E\; ^\; \{3\; \backslash \; over\; 2\}.\}$

Это желательно для равноотстоящих угловых моментов. Если следить за константами, интервал будет ħ, поэтому угловой момент должен быть целым кратным ħ,

$L\; =\; n\; h\; 2\; \pi \; =\; n\; \hslash .\; \{\backslash \; displaystyle\; L\; =\; \{nh\; \backslash \; over\; 2\; \backslash \; pi\}\; =\; n\; \backslash \; hbar\; ~.\}$

Так Бор пришел к его модели.

Подстановка выражения для скорости дает уравнение для r через n:

$meke\; Z\; e\; 2\; merr\; =\; n\; \hslash \; \{\backslash \; displaystyle\; m\; \_\; \{\backslash \; text\; \{e\}\}\; \{\backslash \; sqrt\; \{\backslash \; dfrac\; \{k\_\; \{\backslash \; text\; \{e)\; \}\}\; Ze\; ^\; \{2\}\}\; \{m\; \_\; \{\backslash \; text\; \{e\}\}\; r\}\}\}\; r\; =\; n\; \backslash \; hbar\}$

так, чтобы допустимый радиус орбиты при любом n был:

$rn\; =\; n\; 2\; \hslash \; 2\; Z\; kee\; 2\; me\; \{\backslash \; displaystyle\; r\_\; \{n\}\; =\; \{n\; ^\; \{2\}\; \backslash \; hbar\; ^\; \{2\}\; \backslash \; over\; Zk\; \_\; \{\backslash \; mathrm\; \{e\}\}\; e\; ^\; \{2\}\; m\; \_\; \{\backslash \; mathrm\; \{e\}\}\; \}\}$

Наименьшее возможное значение r в атоме водорода (Z = 1) называется радиусом Бора и равно:

$r\; 1\; =\; \hslash \; 2\; kee\; 2\; me\; \approx \; 5,29\; \times \; 10–11\; м\; \{\; \backslash \; displaystyle\; r\_\; \{1\}\; =\; \{\backslash \; hbar\; ^\; \{2\}\; \backslash \; over\; k\; \_\; \{\backslash \; mathrm\; \{e\}\}\; e\; ^\; \{2\}\; m\; \_\; \{\backslash \; mathrm\; \{e\}\}\}\; \backslash \; приблизительно\; 5,29\; \backslash \; times\; 10\; ^\; \{\; -\; 11\}\; \backslash \; mathrm\; \{m\}\}$

Энергия n-го уровня для любого атома определяет радиусом и квантовым числом:

$E\; =\; -\; Z\; kee\; 2\; 2\; rn\; =\; -\; Z\; 2\; (kee\; 2)\; 2\; меня\; 2\; \hslash \; 2\; N\; 2\; \approx \; -\; 13,6\; Z\; 2\; N\; 2\; e\; V\; \{\backslash \; displaystyle\; E\; =\; -\; \{Zk\; \_\; \{\backslash \; mathrm\; \{e\}\}\; e\; ^\; \{2\}\; \backslash \; over\; 2r\_\; \{n\}\}\; =\; -\; \{Z\; ^\; \{2\}\; (\; k\; \_\; \{\backslash \; mathrm\; \{e\}\}\; e\; ^\; \{2\})\; ^\; \{2\}\; m\; \_\; \{\backslash \; mathrm\; \{e\}\}\; \backslash \; ове\; r\; 2\; \backslash \; hbar\; ^\; \{2\}\; n\; ^\; \{2\}\}\; \backslash \; приблизительно\; \{-\; 13.6Z\; ^\; \{2\}\; \backslash \; over\; n\; ^\; \{2\}\}\; \backslash \; mathrm\; \{эВ\}\}$

Электрон на самом низком энергетическом уровне водорода (n = 1), следовательно, имеет примерно на 13,6 эВ меньше энергии, чем неподвижный электрон, бесконечно удаленный от ядра. Следующий уровень энергии (n = 2) равен −3,4 эВ. Третий (n = 3) равен −1,51 эВ и так далее. Для больших значений энергии связи высоковозбужденного атома с одним электроном на большой круговой орбите вокруг остальной части атома. Формула также совпадает с произведением Уоллиса.

Комбинация естественных констант в формуле энергии называется энергией Ридберга (R E):

$RE\; =\; (kee\; 2)\; 2\; я\; 2\; \hslash \; 2\; \{\backslash \; displaystyle\; R\; \_\; \{\backslash \; mathrm\; \{E\}\}\; =\; \{(k\; \_\; \{\backslash \; mathrm\; \{e\}\}\; e\; ^\; \{2\})\; ^\; \{2\}\; m\; \_\; \{\backslash \; mathrm\; \{e\}\}\; \backslash \; over\; 2\; \backslash \; hbar\; ^\; \{2\}\}\; \}$

Это выражение поясняется его интерпретацией в комбинациях, которые образуют более натуральных единиц :

$mec\; 2\; \{\backslash \; displaystyle\; \backslash ,\; m\; \_\; \{\backslash \; mathrm\; \{e\}\}\; c\; ^\; \{2\}\}$- энергия массы покоя электрона (511 кэВ)

$kee\; 2\; \hslash \; c\; =\; \alpha \; \approx \; 1\; 137\; \{\backslash \; displaystyle\; \backslash ,\; \{k\; \_\; \{\backslash \; mathrm\; \{e\}\}\; e\; ^\; \{2\}\; \backslash \; over\; \backslash \; hbar\; c\}\; =\; \backslash \; alpha\; \backslash \; приблизительно\; \{1\; \backslash \; over\; 137\}\}$- постоянная тонкой структуры

$RE\; =\; 1\; 2\; (mec\; 2)\; \alpha \; 2\; \{\backslash \; displaystyle\; \backslash ,\; R\; \_\; \{\; \backslash \; mathrm\; \{E\}\}\; =\; \{1\; \backslash \; over\; 2\}\; (m\; \_\; \{\backslash \; mathrm\; \{e\}\}\; c\; ^\; \{2\})\; \backslash \; alpha\; ^\; \{2\}\}$

Письмо это вывод с Если предположить, что ядро вращается вокруг одного электрона, мы можем обобщить этот результат, допустив, что ядро ​​имеет заряд q = Ze, где Z - атомный номер . Теперь это даст нам уровни энергии для водородных («водородоподобных») элементов, которые могут служить грубым приближением по порядку фактических уровней энергии. Итак, для ядер с Z протонами уровней энергии (в грубом приближении):

$E\; n\; =\; -\; Z\; 2\; RE\; n\; 2\; \{\backslash \; displaystyle\; E\_\; \{n\}\; =\; -\; \{Z\; ^\; \{2\}\; R\; \_\; \{\backslash \; mathrm\; \{E\}\; \}\; \backslash \; over\; n\; ^\; \{2\}\}\}$

Реальные уровни энергии не могут быть решены аналитически для более чем одного электрона (см. задача о n телах ), потому что на электроны влияют не только ядро ​​, но также взаимодействуют друг с другом посредством кулоновской силы.

. Когда Z = 1 / α (Z ≈ 137), движение становится в высшей степени релятивистским, и Z отменяет α в R; энергия орбиты начинает быть сопоставимой с энергией покоя. Достаточно большие ядра, если бы они были стабильными, уменьшили бы свой заряд, создав связанный электрон из вакуума, выбрасывая позитрон на бесконечность. Это теоретическое явление экранирования электромагнитного заряда, которое предсказывает максимальный заряд ядра. Эмиссия таких позитронов наблюдалась при столкновениях тяжелых ионов с образованием временных сверхтяжелых ядер.

Формула Бора правильно использует приведенную массу электрона и протона во всех ситуациях, вместо этого массы электрона,

$m\; красный\; =\; mempme\; +\; mp\; =\; me\; 1\; 1\; +\; me\; /\; mp.\; \{\backslash \; displaystyle\; m\; \_\; \{\backslash \; text\; \{red\}\}\; =\; \{\backslash \; frac\; \{m\; \_\; \{\backslash \; mathrm\; \{e\}\}\; m\; \_\; \{\backslash \; mathrm\; \{p\}\}\}\; \{m\; \_\; \{\backslash \; mathrm\; \{e\}\}\; +\; m\; \_\; \{\backslash \; mathrm\; \{p\}\; \}\}\}\; =\; m\; \_\; \{\backslash \; mathrm\; \{e\}\}\; ~\; \{\backslash \; frac\; \{1\}\; \{1\; +\; m\; \_\; \{\backslash \; mathrm\; \{e\}\}\; /\; m\; \_\; \{\backslash \; mathrm\; \{p\}\}\}\}\; ~.\}$

Однако эти числа почти одинаковы из-за гораздо большей массы протона, примерно в 1836,1 раз больше массы электрона, так что приведенная масса в системе равна массе электрона, умноженной на константу 1836,1 / (1 + 1836,1) = 0,99946. Этот факт исторически важен для того, чтобы убедить Резерфорда в важности модели Бора, поскольку он объясняет тот факт, что частоты линий в спектрах однократно ионизованного гелия отличаются от частот линий водорода не ровно в 4 раза, а скорее в 4 раза. умноженное на отношение приведенной массы для систем водорода и гелия, которое было намного ближе к экспериментальному соотношению, чем точно 4.

Для позитронияв формуле также используется приведенная масса, но в данном случае это в точности электрона, деленная на 2. При любом значении радиуса и позитроне с половинной скоростью вокруг своего центра масс, и каждый из них имеет только четверть кинетической скорости. энергия. Полная кинетическая энергия вдвое меньше, чем у отдельного электрона, движущегося вокруг тяжелого ядра.

$E\; n\; =\; RE\; 2\; n\; 2\; \{\backslash \; displaystyle\; E\_\; \{n\}\; =\; \{R\; \_\; \{\backslash \; mathrm\; \{E\}\}\; \backslash \; over\; 2n\; ^\; \{2\}\}\; ~~~~~~\}$( позитроний)

Формула Ридберга

Формула Ридберга, которая была эмпирически известна до формулы Бора, изучая теорию Бора как описывающая энергия переходов или квантовых скачков между орбитальными энергетическими уровнями. Формула Бора дает числовое значение уже известной и измеренной Ридберга, но с точки зрения более фундаментальных констант природы, включая заряд электрона и постоянную Планка.

Когда электрон перемещается с уровня энергии на более высокий, затем он перескакивает назад на каждый уровень, пока не достиг исходной позиции, что приводит к испусканию фотона . Используя формулу для различных уровней света водорода, можно определить длину волны, которая может излучать атом водорода.

Энергия фотона, испускаемого атомом водорода, определяется разностью двух уровней водорода:

$E\; =\; E\; i\; -\; E\; f\; =\; RE\; (1\; nf\; 2\; -\; 1\; ni\; 2)\; \{\backslash \; displaystyle\; E\; =\; E\_\; \{i\}\; -E\_\; \{f\}\; =\; R\; \_\; \{\backslash \; mathrm\; \{E\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{n\_\; \{f\}\; ^\; \{2\}\}\}\; -\; \{\backslash \; frac\; \{1\}\; \{n\_\; \{i\}\; ^\; \{2\; \}\}\}\; \backslash \; right)\; \backslash ,\}$

где n f - конечный уровень энергии, а n i - начальный уровень.

энергия фотона равна

$E\; =\; hc\; \lambda ,\; \{\backslash \; displaystyle\; E\; =\; \{\backslash \; frac\; \{hc\}\; \{\backslash \; lambda\}\},\; \backslash ,\}$

длина волны испускаемого фотона равна

$1\; \lambda \; =\; R\; (1\; nf\; 2\; -\; 1\; ni\; 2).\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{\backslash \; lambda\}\}\; =\; R\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{n\_\; \{f\}\; ^\; \{2\}\}\}\; -\; \{\backslash \; frac\; \{1\}\; \{n\_\; \{i\}\; ^\; \{\; 2\}\}\}\; \backslash \; справа).\; \backslash ,\}$

Это известно как формула Ридберга, а константа Ридберга R равна R E / hc, или R E / 2π в натуральных единицах. Эта формула была известна в девятнадцатом веке ученым, изучающим спектроскоп, но до Бора не было теоретического объяснения этой формы или теоретического предсказания значения R. Фактически, вывод Бора постоянной истории, а также сопутствующее использование формулы Бора с экспериментально наблюдаемыми спектральными линиями Лаймана (nf= 1), Бальмера (nf= 2) и Пашена (nf= 3) и успешное теоретическое предсказание других линий, которые еще не наблюдались, были одними из причин, по которой его модель была немедленно принята.

Чтобы применить к атомам с более чем одним электроном, формулу Ридберга можно изменить, заменив Z на Z - b или n на n - b, где b - константа, представляющая эффект экранирования из-за внутренней оболочки и другие электроны (см. Электронная оболочка и более позднее обсуждение «Оболочечной модели атома» ниже). Это было установлено эмпирически до того, как Бор представил свою модель.

Оболочечная модель (более тяжелые атомы)

Бор расширил модель водорода, чтобы дать приблизительную модель для более тяжелых атомов. Это дало физическую картину, которая впервые воспроизводила многие известные атомные свойства.

У более тяжелых элементов больше протонов в ядре и больше электронов, чтобы нейтрализовать заряд. Идея Бора заключалась в том, что дискретная орбита могла удерживать только определенное количество электронов. После того, как эта орбита заполнится, нужно будет использовать следующий уровень. Это дает атому структуру оболочки , в которой каждая оболочка соответствует орбите Бора.

Эта модель даже более приближена, чем она рассматривает электроны в каждой оболочке как невзаимодействующие. Но отталкивание электронов отчасти учитывается явлением экранирования. Электроны на внешних орбитах не вращаются вокруг внутреннего ядра, поэтому эффективный заряд Z, который они ощущают, уменьшаются на количество электронов на внутренней орбите.

Например, у атома лития два электрона находятся на самой нижней 1-й орбите, и эти электроны находятся на Z = 2. Каждый из них видит заряд ядра Z = 3 минус экранирующий эффект другого, что грубо снижает ядерный заряд на 1 ед. Это означает, что самые внутренние электроны вращаются на 1/2 радиуса Бора. Самый внешний электрон на орбите находится на расстоянии примерно одного радиуса, поскольку два внутренних электрона уменьшают заряд ядра 2. Этот внешний электрон должен находиться на расстоянии примерно одного радиуса Бора от ядра. Электроны сильно отталкиваются друг от друга, описание эффективного заряда очень приблизительное; эффективный заряд Z обычно не оказывается целым. Но закон Мозли экспериментально исследует самую внутреннюю пару электронов и показывает, что они действительно видят ядерный заряд приблизительно Z - 1, в то время как самый внешний электрон в атоме или ионе только одним электроном на внешней оболочке орбит ядро ​​с эффективным зарядом Z-k, где k - полное количество электронов во внутренних оболочках.

Оболочечная модель смогла качественно многие загадочные свойства, которые были систематизированы в конце 19 века в периодической таблице элементов. Одним из свойств был размер атомов, который можно определить методом измерения вязкости газов и плотности чистых твердых твердых веществ. Атомы имеют тенденцию уменьшаться в размерах вправо в периодической таблице и становиться намного больше в следующей таблице. Атомы справа от таблицы стремятся получить электроны, а атомы слева - их терять. Каждый элемент в последнем столбце таблицы химически инертен (благородный газ ).

В модели оболочки это явление объясняется заполнением оболочки. Последовательные атомы становятся меньше, потому что они заполняют орбиты одного и того же размера, пока орбита не заполнится, и в этот момент следующий атом в таблице имеет связанный внешний электрон, заставляющий его расширяться. Первая боровская орбита заполнена, когда на ней есть два электрона, что объясняет, почему гелий инертен. Вторая орбита пропускает восемь электронов, и когда она заполнена, атом становится неоновым, снова инертным. Третья орбиталь снова содержит восемь, за исключением того, что в более правильной трактовке Зоммерфельда (воспроизведенной в современной квантовой механике) есть лишние "d" электроны. Третья орбита может содержать дополнительные 10 электронов, но эти позиции не заполняются до тех пор, пока не заполнены еще несколько орбиталей со следующего уровня (заполнение n = 3 d орбиталей дает 10 переходных элементов ). Неравномерное заполнение - это эффект взаимодействия между электронами, которые не учитываются в моделях Бора, ни в моделях Зоммерфельда и которые трудно вычислить даже в современной трактовке.

Закон и расчет Мозли (K-альфа-рентгеновские эмиссионные линии)

Нильс Бор сказал в 1962 году: «Видите ли, на самом деле работа Резерфорда не принималась всерьез. Мы не можем понять сегодня, но его вообще не воспринимают всерьез. Об этом не упоминается ни в каком месте. Великая перемена произошла от Мозли ».

В 1913 г. Генри Мозли обнаружил эмпирическую связь между сильнейшими X-лучевая линия, испускаемая атомами при электронной бомбардировке (тогда известная как линия K-alpha ), и их атомный номер Z. Было обнаружено, что эмпирическая формула Мозли выводится из формулы Ридберга и Бора (Мозли фактическиет только Эрнест Резер и Антониус Ван ден Брук в терминах моделей). Два дополнительных предположения, что [1] генгеновская линия произошла от рентгеновского излучения между энергетическими уровнями с квантовыми числами 1 и 2, и [2], что атомный номер Z при использовании в формуле для уменьшения на 1 до (Z - 1).

Мозли написал Бору, озадаченный своими результатами, но Бор не смог помочь. В то время он думал, что постулируемая самая внутренняя "K" -оболочка электронов должна иметь по крайней мере четыре электрона, а не два, которые точно объяснили бы результат. Поэтому Мозли опубликовал свои результаты без теоретического объяснения.

Позже люди поняли, эффект вызван экранированием заряда внутренней оболочкой всего 2 электрона. В эксперименте один из самых внутренних электронов в атоме выбивается, которая содержит оставшийся электрон. Затем эта вакансия заполняется электроном со следующей орбиты, у которой n = 2. Но n = 2 электрона видят эффективный заряд Z - 1, который является подходящим для заряда ядра, когда один электрон остается на самой нижней боровской орбите, чтобы экранировать заряд ядра. + Z, и понижает его на - 1 (из-за того, что отрицательный заряд электрона экранирует положительный заряд ядра). Энергия, полученная электроном, падающим со второй оболочки на первую, дает закон Мозли для линий K-альфа,

$E\; =\; h\; \nu \; =\; E\; i\; -\; E\; f\; =\; RE\; (Z\; -\; 1)\; 2\; (1\; 1\; 2\; -\; 1\; 2\; 2)\; \{\backslash \; displaystyle\; E\; =\; h\; \backslash \; nu\; =\; E\_\; \{i\}\; -E\_\; \{f\}\; =\; R\; \_\; \{\backslash \; mathrm\; \{E\}\}\; (Z-1)\; ^\; \{2\}\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{1\; ^\; \{2\}\}\}\; -\; \{\backslash \; frac\; \{1\}\; \{2\; ^\; \{2\}\}\}\; \backslash \; right)\; \backslash ,\}$

или

$f\; =\; \nu \; =\; R\; v\; (3\; 4)\; (\; Z\; -\; 1)\; 2\; =\; (2,46\; \times \; 10\; 15\; Гц)\; (Z\; -\; 1)\; 2.\; \{\backslash \; displaystyle\; f\; =\; \backslash \; nu\; =\; R\; \_\; \{\backslash \; mathrm\; \{v\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{3\}\; \{4\; \}\}\; \backslash \; right)\; (Z-1)\; ^\; \{2\}\; =\; (2,46\; \backslash \; times\; 10\; ^\; \{15\}\; \backslash \; operatorname\; \{Hz\})\; (Z-1)\; ^\; \{2\}.\}$

Здесь Rv= RE/h- постоянная Ридберга, выраженная частота, равной 3,28 x 10 Гц. Для значений Z 11 и 31 это последнее соотношение было получено эмпирическим путем Мозли на простом (линейном) графике зависимости квадратного корня из частот рентгеновского излучения от атомного номера (однако для серебра Z = 47 экспериментально полученное значение срок проверки заменить на 0,4). Несмотря на свою ограниченную применимость, закон Мозли не только установил объективное значение атомного числа (см. Генри Мозли для подробностей), но, как отметил Бор, он также сделал больше, чем вывод Ридберга, установить справедливость Резерфорда. / Ван ден Брук / Ядерная модель атома Бора, в которой атомный номер (место в периодической таблице) обозначает целые единицы заряда ядра.

Линия K-alpha времен Мозли теперь известна как пара близких линий, записанных как (Kα1и Kα2) в нотации Зигбана.

Недостатки

Модель Бора дает неверное значение L = ħ для орбитального углового момента основного состояния: угловой момент в истинном основном состоянии известен из экспериментов, что равенство нулю. Ментальные образы несколько неудач на этих уровнях масштаба, электрон на самой низкой стадии «орбитали» без орбитального момента можно рассматривать как вообще не вращающийся «вокруг» ядра, а просто плотно обтекающий его в эллипсе с нулевой площадью (это можно изобразить как « вперед и назад », не поражая ядро ​​и не взаимодействуя с ним). Это воспроизводится только в более сложной полуклассической обработке, такой как у Зоммерфельда. Тем не менее, даже самая сложная полуклассическая модель не может объяснить того факта, что состояние с наименьшей энергией является сферически симметричным - оно не указывает в каком-либо конкретном направлении.

Тем не менее, в современной полностью квантовой трактовке фазового пространства правильная деформация (осторожное полное растяжение) полуклассического результата регулирует значение углового момента до правильного эффективного. Как следствие, выражение физического основного состояния получается посредством сдвига выражения исчезающего квантового углового момента, которое соответствует сферической симметрии.

В современной квантовой механике электрон в водороде - это сферическое облако вероятности, которое становится плотнее около ядра. Константа скорости распада вероятности в водороде равна обратной величине радиуса Бора, но поскольку Бор работал с круговыми орбитами, а не с эллипсами с нулевой площадью, тот факт, что эти два числа точно совпадают, считается «совпадением». (Однако между полуклассическим и полным квантово-механическим подходом к изучению атома обнаруживается много таких совпадений; они включают идентичные уровни энергии в атоме водорода и вывод постоянной тонкой структуры, которая возникает из релятивистская модель Бора – Зоммерфельда (см. ниже), которая, как оказалось, соответствует совершенно другой концепции в полной современной квантовой механике).

Модель Бора также затруднена с объяснением или не может объяснить:

• Большая часть спектров более крупных атомов. В лучшем случае он может делать прогнозы относительно K-альфа и некоторых L-альфа-спектров рентгеновского излучения для более крупных атомов, если сделаны два дополнительных специальных предположения (см. закон Мозли над). Спектры излучения для атомов с одним электроном на внешней оболочке (атомы в группе лития ) также могут быть приблизительно предсказаны. Кроме того, если известны эмпирические коэффициенты электронно-ядерного экранирования для многих атомов, многие другие спектральные линии могут быть выведены из информации в аналогичных атомах различных элементов с помощью принципов комбинации Ритца – Ридберга (см. формула Ридберга ). Все эти методы по существу используют ньютоновскую картину энергетического потенциала атома Бора.
• относительные интенсивности спектральных линий; хотя в некоторых простых случаях формула Бора или ее модификации могли дать разумные оценки (например, расчеты Крамерса для эффекта Штарка ).
• Существование тонкой структуры и сверхтонкая структура в спектральных линиях, которые, как известно, связаны с различными релятивистскими и тонкими эффектами, а также с осложнениями, связанными с электронным спином.
• Эффект Зеемана - изменения в спектральных линиях из-за внешних магнитных полей ; они также связаны с более сложными квантовыми принципами, взаимодействующими со спиновыми и орбитальными магнитными полями электронов.
• Модель также нарушает принцип неопределенности в том смысле, что он считает, что у электронов есть известные орбиты и местоположение, две вещи, которые нельзя измерить одновременно.
• Дублеты и триплеты: появляются в спектрах некоторых атомов: очень близкие пары линий. Модель Бора не может сказать почему некоторые энергетические уровни должны находиться очень близко друг к другу.
• Многоэлектронные атомы: d у меня нет уровня энергии, предсказанного м одель. Это не работает для (нейтрального) гелия.

.

Уточнения

Эллиптические орбиты с той же энергией и квантованным угловым моментом

Было предложено несколько усовершенствований модели Бора, в первую очередь Зоммерфельда модель или модель Бора - Зоммерфельда, которая предполагала, что электроны движутся по эллиптическим орбитам вокруг ядра, а не по круговым орбитам модели Бора. Эта модель дополняет условие квантованного углового момента модели Бора дополнительным условием радиального квантования, условием квантования Вильсона - Зоммерфельда

$\int \; 0\; T\; prdqr\; =\; nh\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{\; 0\}\; ^\; \{T\}\; p\_\; \{r\}\; \backslash ,\; dq\_\; \{r\}\; =\; nh\; \backslash ,\}$

где p r - это радиальный импульс, канонически сопряженный с координатой q, который представляет собой радиальное положение, а T - один полный период обращения. Интеграл - это действие в координатах действие-угол. Это условие, предложенное принципом соответствия, является единственно возможным, квантовыми числами являются адиабатическими инвариантами.

Модель Бора - Зоммерфельда была в корне противоречивой и приводила ко многим парадоксам. Магнитное квантовое число измеряет наклон плоскости орбиты относительно плоскости xy и может принимать только несколько дискретных значений. Это противоречило очевидному факту, что атом можно поворачивать в разные стороны относительно координат без ограничений. Квантование Зоммерфельда может быть в разных канонических координатах и ​​иногда дает разные ответы. Включение поправки на излучение было трудным, потому что требовалось найти координаты действие-угол для комбинированной системы излучение / атом, что затруднительно, когда излучение позволяет выходить. Вся теория не распространяется на неинтегрируемые движения. В конце концов, модель была заменена современной квантово-механической обработкой атома водорода, полученной впервые Вольфганг Паули в 1925 году, используя Матричная механика Гейзенберга . Современная картина атома водорода на атомных орбиталях волновой механики, которые Эрвин Шредингер разработал в 1926 году.

Однако это Нельзя сказать, что модель Бора-Зоммерфельда не успеха. Расчеты, основанные на модели Бора - Зоммерфельда, смогли точно объяснить ряд более сложных атомных спектральных эффектов. Например, вплоть до возмущений первого порядка модель Бора и квантовая механика делают одинаковые предсказания для расщепления спектральной линии в эффекте Штарка. Однако при возмущении более высокого порядка модель Бора и квантовая механика различаются, и измерения эффекта Штарка при высокой напряженности поля помогли подтвердить правильность квантовой механики над моделью Бора. Преобладающая теория, стоящая за этим различием, заключается в формех орбиталей электронов, которые меняются в зависимости от энергетического состояния электрона.

Условия квантования Бора - Зоммерфельда вызывают вопросы в современной математике. Согласованное условие квазиклассического квантования требует определенного типа структурного пространства, что накладывает топологические ограничения на тип симплектических совокупностей, которые можно квантовать. В частности, симплектическая форма должна быть форма кривизны соединение линейного пучка эрмитова , который называется предварительное квантование.

Модель химического связи

Нильс Бор модель атома и модель химической связи. Согласно его модели для двухатомной молекулы, электроны молекулы образуют вращающееся кольцо, плоскость которого перпендикулярна оси молекулы и равноудалена от ядер элементов. Динамическое равновесие молекулярной системы достигается за счет баланса сил между притяжения ядер к плоскости электронов и силами взаимного отталкивания ядер. Модель друг химической связи Бора учитывала кулоновское отталкивание - электроны в кольце находятся на максимальном расстоянии от друга.

См. Также

1913 г. в науке Константа Бальмера Эксперимент Франка - Герца предоставил раннюю поддержку модели Бора.

Модель атома свободного падения Эффект инертной пары адекватно объясняется с помощью модели Бора. Введение в квантовую механику Теоретическое и экспериментальное обоснование уравнения Шредингера

Сноски

Первоисточники

• Нильс Бор (1913). «О строении атомов и молекул, часть I» (PDF). Философский журнал. 26 (151): 1–24. Bibcode : 1913PMag... 26.... 1B. doi : 10.1080 / 14786441308634955.
• Нильс Бор (1913). «О строении атомов и молекул, часть II. Системы, содержащие только одно ядро ​​» (PDF). Философский журнал. 26 (153): 476–502. Bibcode : 1913PMag... 26..476B. doi : 10.1080 / 14786441308634993.
• Нильс Бор (1913). «О строении атомов и молекул, часть III. Системы, содержащие несколько ядер ». Философский журнал. 26 : 857–875. Bibcode : 1913PMag... 26..857B. doi : 10.1080 / 14786441308635031.
• Нильс Бор (1914). «Спектры гелия и водорода». Природа. 92 (2295): 231–232. Bibcode : 1913Natur..92.. 231B. doi : 10.1038 / 092231d0.
• Нильс Бор (1921). «Атомная структура». Природа. 107 (2682): 104–107. Bibcode : 1921Natur.107..104B. doi : 10.1038 / 107104a0.
• A. Эйнштейн (1917). "Zum Quantensatz von Sommerfeld und Epstein". Verhandlungen der Deutschen Physikalischen Gesellschaft. 19 : 82–92. Перепечатано в сборнике документов Альберта Эйнштейна, переводчика А. Энгеля, (1997) Princeton University Press, Princeton. 6 стр. 434. (дает элегантную переформулировку условий квантования Бора - Зоммерфельда, а также понимание квантования неинтегрируемых (хаотических) динамических систем.)

Дополнительная литература

• Линус Карл Полинг (1970). «Глава 5-1». Общая химия (3-е изд.). Сан-Франциско: W.H. Freeman Co.
  • Перепечатка: Линус Полинг (1988). Общая химия. Нью-Йорк: Dover Publications. ISBN 0-486-65622-5.
• Джордж Гамов (1985). «Глава 2». Тридцать лет, потрясших физику. Dover Publications.
• Вальтер Дж. Леманн (1972). «Глава 18». Атомная и молекулярная структура: развитие наших представлений. Джон Уайли и сыновья. ISBN 0-471-52440-9.
• Пол Типлер и Ральф Ллевеллин (2002). Современная физика (4-е изд.). В. Х. Фриман. ISBN 0-7167-4345-0.
• Клаус Хентшель : Elektronenbahnen, Quantensprünge und Spektren, в: Charlotte Bigg Jochen Hennig (ред.) Atombilder. Ikonografien des Atoms in Wissenschaft und Öffentlichkeit des 20. Jahrhunderts, Göttingen: Wallstein-Verlag 2009, pp. 51–61
• Стивен и Сьюзан Зумдаль (2010). «Глава 7.4». Химия (8-е изд.). Брукс / Коул. ISBN 978-0-495-82992-8.
• Хельге Краг (2011). «Концептуальные возражения против атомной теории Бора - есть ли у электронов« свобода воли »?». Европейский физический журнал H. 36(3): 327–352. Bibcode : 2011EPJH... 36..327K. doi : 10.1140 / epjh / e2011-20031-x.

ние ссылки

• Стоячие волны в атомной модели Бора Интерактивное моделирование для интуитивного объяснения условия квантования стоячих волн в Атомный режим Бора

На Викискладе есть материалы, связанные с моделью Бора.