B-сплайн

Функция сплайна B-сплайн с контрольными точками / контрольным многоугольником и отмеченными кривыми компонентов

В математическое подполе численного анализа, B-сплайн или базисный сплайн - это сплайн функция, имеющая минимальное значение поддерживают в отношении заданной степени, гладкости и раздела домена. Любая сплайн-функция заданной степени может быть выражена как линейная комбинация B-сплайнов этой степени. Кардинальные B-шлицы имеют узлы, равноудаленные друг от друга. B-сплайны могут использоваться для аппроксимации кривой и численного дифференцирования экспериментальных данных.

В автоматизированном проектировании и компьютерной графике сплайн-функции строятся как линейные комбинации B-сплайнов с набором контрольных точек.

• 1 Введение
• 2 Определение
• 3 Свойства
  • 3.1 Кардинальный B-сплайн
  • 3.2 P-сплайн
• 4 Производные выражения
• 5 Моменты одномерных B-сплайнов
• 6 Связь с кусочным / составным Безье
• 7 Аппроксимация кривой
• 8 Компьютерное проектирование и компьютерная графика
• 9 NURBS
• 10 См. Также
• 11 Примечания
• 12 Ссылки
• 13 Дополнительная литература
• 14 Внешние ссылки

Термин «B-сплайн» был придуман Исааком Якобом Шенбергом и является сокращением от слова «базис». сплайн. Сплайн-функция порядка $n\; \{\backslash \; displaystyle\; n\}$- это кусочно полиномиальная функция степени $n\; -\; 1\; \{\backslash \; displaystyle\; n-\; 1\}$в переменной $x\; \{\backslash \; displaystyle\; x\}$. Места, где встречаются части, называются узлами. Ключевым свойством сплайн-функций является то, что они и их производные могут быть непрерывными, в зависимости от кратности узлов.

B-сплайны порядка $n\; \{\backslash \; displaystyle\; n\}$- это базисные функции для сплайн-функций того же порядка, определенных для одних и тех же узлов, что означает, что все возможные сплайн-функции могут быть построены из линейной комбинации B-сплайнов, и существует только одна уникальная комбинация для каждой сплайн-функции.

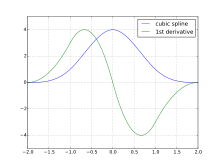
Кардинальный квадратичный B-сплайн с вектор узла (0, 0, 0, 1, 2, 3, 3, 3) и контрольные точки (0, 0, 1, 0, 0) и его первая производная Кардинальный кубический B-сплайн с вектором узла ( −2, −2, −2, −2, −1, 0, 1, 2, 2, 2, 2) и контрольные точки (0, 0, 0, 6, 0, 0, 0) и его первая производная Кардинальный B-сплайн четвертой степени с вектором узлов (0, 0, 0, 0, 0, 1, 2, 3, 4, 5, 5, 5, 5, 5) и контрольными точками (0, 0, 0, 0, 1, 0, 0, 0, 0) и его первая и вторая производные

Сплайн порядка $n\; \{\backslash \; displaystyle\; n\}$представляет собой кусочно полином функция степени $n\; -\; 1\; \{\backslash \; displaystyle\; n-1\}$в переменной $x\; \{\backslash \; d\; isplaystyle\; x\}$. Значения $x\; \{\backslash \; displaystyle\; x\}$там, где встречаются части многочлена, называются узлами и обозначаются $t\; 0,\; t\; 1,\; t\; 2,\dots ,\; tn\; \{\backslash \; displaystyle\; t\_\; \{\; 0\},\; t\_\; \{1\},\; t\_\; \{2\},\; \backslash \; ldots,\; t\_\; \{n\}\}$и отсортированы в порядке неубывания. Когда узлы различны, первые $n\; -\; 2\; \{\backslash \; displaystyle\; n-2\}$производные частей многочлена являются непрерывными для каждого узла. Когда $r\; \{\backslash \; displaystyle\; r\}$узлы совпадают, тогда только первые $n\; -\; r\; -\; 1\; \{\backslash \; displaystyle\; nr-1\}$производные сплайна являются непрерывно через этот узел.

Для данной последовательности узлов существует, с точностью до коэффициента масштабирования, уникальный сплайн $B\; i,\; n\; (x)\; \{\backslash \; displaystyle\; B\_\; \{i,\; n\}\; (x)\}$удовлетворение

Если мы добавим дополнительное ограничение, которое $\sum \; i\; B\; i,\; n\; (x)\; =\; 1\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{\; i\}\; B\_\; \{i,\; n\}\; (x)\; =\; 1\}$для всех $x\; \{\backslash \; displaystyle\; x\}$между первым и последним узлами, затем коэффициент масштабирования $B\; i,\; n\; (x)\; \{\backslash \; displaystyle\; B\_\; \{i,\; n\}\; (x)\}$становится фиксированным. Результирующие сплайновые функции $B\; i,\; n\; (x)\; \{\backslash \; displaystyle\; B\_\; \{i,\; n\}\; (x)\}$называются B-сплайнами.

В качестве альтернативы, B-сплайны могут быть определены путем построения с помощью формулы рекурсии Кокса – де Бора. Дана последовательность узлов $\dots ,\; t\; 0,\; t\; 1,\; t\; 2,\dots \; \{\backslash \; displaystyle\; \backslash \; ldots,\; t\_\; \{0\},\; t\_\; \{1\},\; t\_\; \{2\},\; \backslash \; ldots\}$, тогда B-сплайны порядка 1 определяются как

Они удовлетворяют $\sum \; i\; B\; i,\; 1\; (x)\; =\; 1\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{i\}\; B\_\; \{i,\; 1\}\; (x)\; =\; 1\}$для всех $x\; \{\backslash \; displaystyle\; x\}$, потому что для любого $x\; \{\backslash \; displaystyle\; x\}$ровно один из $B\; i,\; 1\; (x)\; =\; 1\; \{\backslash \; displaystyle\; B\_\; \{i,\; 1\}\; (x)\; =\; 1\}$, и все другие равны нулю.

B-сплайны более высокого порядка определяются рекурсией

$B\; i,\; k\; +\; 1\; (x):\; =\; \omega \; i,\; k\; (x)\; B\; i,\; k\; (x)\; +\; [1\; -\; \omega \; i\; +\; 1,\; К\; (Икс)]\; В\; я\; +\; 1,\; К\; (Икс),\; \{\backslash \; Displaystyle\; В\_\; \{я,\; к\; +\; 1\}\; (х):\; =\; \backslash \; omega\; \_\; \{я,\; к\}\; (х)\; В\_\; \{я,\; к\; \}\; (x)\; +\; [1-\; \backslash \; omega\; \_\; \{i\; +\; 1,\; k\}\; (x)]\; B\_\; \{i\; +\; 1,\; k\}\; (x),\}$

где

$\omega \; i,\; k\; (x):\; =\; \{x\; -\; titi\; +\; k\; -\; ti,\; ti\; +\; k\; \ne \; ti\; 0\; в\; противном\; случае.\; \{\backslash \; displaystyle\; \backslash \; omega\; \_\; \{i,\; k\}\; (x):\; =\; \{\backslash \; begin\; \{cases\}\; \{\backslash \; frac\; \{x-t\_\; \{i\}\}\; \{t\_\; \{i\; +\; k\}\; -t\_\; \{i\}\}\},\; t\_\; \{\; i\; +\; k\}\; \backslash \; neq\; t\_\; \{i\}\; \backslash \backslash \; 0,\; \{\backslash \; text\; \{else\}\}\; \backslash \; end\; \{cases\}\}.\}$

Функция B-сплайна представляет собой комбинацию гибких полос который проходит через множество точек, называемых контрольными точками, и создает плавные кривые. Эти функции позволяют создавать сложные формы и поверхности и управлять ими с помощью ряда точек. B-сплайн и функции Безье широко применяются в методах оптимизации формы.

B-сплайн порядка $n\; \{\backslash \; displaystyle\; n\}$- это кусочно-полиномиальная функция степени $n\; -\; 1\; \{\backslash \; displaystyle\; n-1\}$в переменной $x\; \{\backslash \; displaystyle\; x\}$. Он определяется в $1\; +\; n\; \{\backslash \; displaystyle\; 1\; +\; n\}$местоположениях $tj\; \{\backslash \; displaystyle\; t\_\; \{j\}\}$, называемых узлами или точками останова, которые должны быть в порядке убывания $tj\; \le \; tj\; +\; 1\; \{\backslash \; displaystyle\; t\_\; \{j\}\; \backslash \; leq\; t\_\; \{j\; +\; 1\}\}$. B-сплайн вносит вклад только в диапазоне между первым и последним из этих узлов и равен нулю в других местах. Если каждый узел разделен одинаковым расстоянием $h\; \{\backslash \; displaystyle\; h\}$(где $h\; =\; tj\; +\; 1\; -\; tj\; \{\backslash \; displaystyle\; h\; =\; t\_\; \{j\; +\; 1\}\; -t\_\; \{\; j\}\}$) от своего предшественника, узловой вектор и соответствующие B-сплайны называются «равномерными» (см. кардинальный B-сплайн ниже).

Для каждого конечного интервала узлов, где он не равен нулю, B-сплайн представляет собой полином степени $n\; -\; 1\; \{\backslash \; displaystyle\; n-1\}$. B-сплайн - это непрерывная функция в узлах. Когда все узлы, принадлежащие B-сплайну, различны, его производные также непрерывны до производной степени $n\; -\; 2\; \{\backslash \; displaystyle\; n-2\}$. Если узлы совпадают при заданном значении $x\; \{\backslash \; displaystyle\; x\}$, непрерывность производного порядка уменьшается на 1 для каждого дополнительного совпадающего узла. B-сплайны могут иметь общие подмножества своих узлов, но два B-сплайна, определенные над одними и теми же узлами, идентичны. Другими словами, B-сплайн однозначно определяется своими узлами.

Различают внутренние узлы и конечные точки. Внутренние узлы покрывают $x\; \{\backslash \; displaystyle\; x\}$-домен, который интересует. Поскольку один B-сплайн уже простирается на $1\; +\; n\; \{\backslash \; displaystyle\; 1\; +\; n\}$узлов, из этого следует, что внутренние узлы необходимо удлинить с помощью $n\; -\; 1\; \{\backslash \; displaystyle\; n-1\}$конечных точек с каждой стороны, чтобы обеспечить полную поддержку первой и последний B-шлиц, влияющий на внутренние интервалы узлов. Значения конечных точек не имеют значения, обычно первый или последний внутренний узел просто повторяется.

Полезность B-сплайнов заключается в том, что любую сплайн-функцию порядка $n\; \{\backslash \; displaystyle\; n\}$на данном наборе узлов можно выразить как линейную комбинацию B-шлицев:

$S\; n,\; t\; (x)\; =\; \sum \; i\; \alpha \; i\; B\; i,\; n\; (x).\; \{\backslash \; displaystyle\; S\_\; \{n,\; \backslash \; mathbf\; \{t\}\}\; (x)\; =\; \backslash \; sum\; \_\; \{i\}\; \backslash \; alpha\; \_\; \{i\}\; B\_\; \{i,\; n\}\; (x).\}$

B-шлицы играют роль базисные функции для пространства сплайн-функций, отсюда и название. Это свойство следует из того факта, что все части имеют одинаковые свойства непрерывности в пределах их индивидуального диапазона поддержки в узлах.

Выражения для полиномиальных частей могут быть получены с помощью рекурсивной формулы Кокса – де Бура.

$B\; i,\; k\; (x):\; =\; x\; -\; titi\; +\; k\; -\; ti\; B\; i,\; k\; -\; 1\; (x)\; +\; ti\; +\; k\; +\; 1\; -\; xti\; +\; k\; +\; 1\; -\; ti\; +\; 1\; B\; i\; +\; 1,\; k\; -\; 1\; (x).\; \{\backslash \; Displaystyle\; В\_\; \{я,\; к\}\; (х):\; =\; \{\backslash \; гидроразрыва\; \{х-т\_\; \{я\}\}\; \{т\_\; \{я\; +\; к\}\; -t\_\; \{я\}\}\}\; В\_\; \{я,\; к-1\}\; (х)\; +\; \{\backslash \; frac\; \{t\_\; \{i\; +\; k\; +\; 1\}\; -x\}\; \{t\_\; \{i\; +\; k\; +\; 1\}\; -t\_\; \{i\; +\; 1\}\}\}\; B\_\; \{i\; +\; 1,\; k-1\}\; (x).\}$

То есть $B\; j,\; 0\; (x)\; \{\backslash \; displaystyle\; B\_\; \{j,\; 0\}\; (x)\}$является кусочно-постоянным единицей или нулем, указывающим, в каком промежутке узла x находится (ноль, если узел j повторяется). Уравнение рекурсии состоит из двух частей:

$x\; -\; titi\; +\; k\; -\; ti\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{x-t\_\; \{i\}\}\; \{t\_\; \{i\; +\; k\}\; -t\_\; \{i\}\}\}\}$

изменяется от нуля до единицы при изменении x от $ti\; \{\backslash \; displaystyle\; t\_\; \{i\}\}$до $ti\; +\; k\; \{\backslash \; displaystyle\; t\_\; \{i\; +\; k\}\}$и

$ti\; +\; k\; +\; 1\; -\; xti\; +\; k\; +\; 1\; -\; ti\; +\; 1\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{t\_\; \{i\; +\; k\; +\; 1\}\; -x\}\; \{t\_\; \{i\; +\; k\; +\; 1\}\; -t\_\; \{i\; +1\}\}\}\}$

изменяется от единицы до нуля при изменении x от $ti\; +\; 1\; \{\backslash \; displaystyle\; t\_\; \{i\; +\; 1\}\}$до $ti\; +\; k\; +\; 1\; \{\; \backslash \; Displaystyle\; t\_\; \{я\; +\; к\; +\; 1\}\}$. Соответствующие B равны нулю вне этих соответствующих диапазонов. Например, $B\; i,\; 1\; (x)\; \{\backslash \; displaystyle\; B\_\; \{i,\; 1\}\; (x)\}$- это треугольная функция, которая равна нулю ниже $x\; =\; ti\; \{\backslash \; displaystyle\; x\; =\; t\_\; \{i\}\}$, переход к единице при $x\; =\; ti\; +\; 1\; \{\backslash \; displaystyle\; x\; =\; t\_\; \{i\; +\; 1\}\}$и обратно к нулю в $и\; далее\; x\; =\; ti\; +\; 2\; \{\backslash \; displaystyle\; x\; =\; t\_\; \{i\; +\; 2\}\}$. Однако, поскольку базисные функции B-сплайна имеют локальную поддержку , B-сплайны обычно вычисляются алгоритмами, которым не нужно оценивать базисные функции, где они равны нулю, например, алгоритм де Бура.

Это соотношение ведет непосредственно к алгоритму BSPLV, закодированному на FORTRAN, который генерирует значения B-сплайнов порядка n в точке x. На следующей схеме показано, как каждая часть порядка n представляет собой линейную комбинацию частей B-сплайнов порядка n-1 слева от нее.

$0\; 0\; 0\; B\; i\; -\; 2,\; 2\; B\; i\; -\; 1,\; 1\; B\; i,\; 0\; B\; i\; -\; 1,\; 2\; B\; i,\; 1\; 0\; B\; i,\; 2\; 0\; 0\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{matrix\}\; 0\; \backslash \; \backslash \; 0\; \backslash \backslash \; 0\; B\_\; \{i-2,2\}\; \backslash \backslash \; B\_\; \{i-1,1\}\; \backslash \backslash \; B\_\; \{i,\; 0\}\; B\_\; \{i-1,2\}\; \backslash \backslash \; B\_\; \{i,\; 1\}\; \backslash \backslash \; 0\; B\_\; \{i,\; 2\}\; \backslash \backslash \; 0\; \backslash \backslash \; 0\; \backslash \backslash \backslash \; end\; \{matrix\}\}\}$

Применение формулы рекурсии с узлами в $(0,\; 1,\; 2,\; 3)\; \{\backslash \; displaystyle\; (0,\; 1,2,3)\}$дает части однородного B-сплайна порядка 3

Эти части показаны на диаграмме. Свойство непрерывности квадратичной сплайн-функции и ее первой производной во внутренних узлах проиллюстрировано следующим образом

$При\; x\; =\; 1,\; B\; 1\; =\; B\; 2\; =\; 0,5;\; d\; B\; 1\; dx\; =\; d\; B\; 2\; dx\; =\; 1\; \{\backslash \; displaystyle\; \{\backslash \; t\_dv\; \{At\}\}\; x\; =\; 1,\; B\_\; \{1\}\; =\; B\_\; \{2\}\; =\; 0,5;\; \{\backslash \; frac\; \{dB\_\; \{1\}\}\; \{dx\}\}\; =\; \{\backslash \; frac\; \{dB\_\; \{2\}\}\; \{dx\}\}\; =\; 1\}$

$При\; x\; =\; 2,\; B\; 2\; =\; B\; 3\; =\; 0,5;\; d\; B\; 2\; dx\; =\; d\; B\; 3\; dx\; =\; -\; 1\; \{\backslash \; displaystyle\; \{\backslash \; t\_dv\; \{At\}\}\; x\; =\; 2,\; B\_\; \{2\}\; =\; B\_\; \{3\}\; =\; 0,5;\; \{\backslash \; frac\; \{dB\_\; \{2\}\}\; \{dx\}\; \}\; =\; \{\backslash \; frac\; \{dB\_\; \{3\}\}\; \{dx\}\}\; =\; -\; 1\}$

Вторая производная B-сплайна степени 2 разрывна в узлах:

$d\; 2\; B\; 1\; dx\; 2\; =\; 1,\; d\; 2\; B\; 2\; dx\; 2\; =\; -\; 2,\; d\; 2\; B\; 3\; dx\; 2\; =\; -\; 1.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; B\_\; \{1\}\}\; \{dx\; ^\; \{2\}\}\}\; =\; 1,\; \{\; \backslash \; frac\; \{d\; ^\; \{2\}\; B\_\; \{2\}\}\; \{dx\; ^\; \{2\}\}\}\; =\; -\; 2,\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; B\_\; \{3\}\}\; \{dx\; ^\; \{2\}\}\}\; =\; -\; 1.\}$

Были предложены более быстрые варианты алгоритма де Бура, но они страдают сравнительно меньшей стабильностью.

Кардинальный B-сплайн

Кардинальный B-сплайн имеет постоянное разделение, h, между узлами. Кардинальные B-сплайны для данного порядка n - это просто сдвинутые копии друг друга. Их можно получить из более простого определения.

$B\; i,\; n,\; t\; (x)\; =\; x\; -\; tihn\; [0,\dots ,\; n]\; (\cdot \; -\; ti)\; +\; n\; -\; 1\; \{\backslash \; displaystyle\; B\_\; \{i,\; n,\; t\}\; (x)\; =\; \{\backslash \; frac\; \{x-t\_\; \{i\}\}\; \{h\}\}\; n\; [0,\; \backslash \; dots,\; n]\; (\backslash \; cdot\; -t\_\; \{i\})\; \_\; \{+\}\; ^\; \{n-1\}\}$

Обозначение «заполнитель» используется для обозначения того, что n-я разделенная разность функции $(t\; -\; x)\; +\; n\; -\; 1\; \{\backslash \; displaystyle\; (tx)\; \_\; \{+\}\; ^\; \{\; n-1\}\}$из двух переменных t и x следует взять, зафиксировав x и учитывая $(t\; -\; x)\; +\; n\; -\; 1\; \{\backslash \; displaystyle\; (tx)\; \_\; \{+\}\; ^\; \{n-1\}\}$как функция только от t.

Кардинальный B-сплайн имеет равномерно распределенные узлы, поэтому интерполяция между узлами равняется свертке со сглаживающим ядром.

Пример, если мы хотим интерполировать три значения между узлами B-сплайна ($b\; \{\backslash \; displaystyle\; \{\backslash \; textbf\; \{b\}\}\}$), мы можем записать сигнал как:

$x\; =\; [b\; 1,\; 0,\; 0,\; b\; 2,\; 0,\; 0,\; b\; 3,\; 0,\; 0,....,\; bn,\; 0,\; 0]\; \{\backslash \; displaystyle\; \{\backslash \; textbf\; \{x\}\}\; =\; [\{\backslash \; textbf\; \{b\}\}\; \_\; \{1\},\; 0,0,\; \{\backslash \; textbf\; \{b\}\}\; \_\; \{2\},\; 0,0,\; \{\backslash \; textbf\; \{b\}\}\; \_\; \{3\},\; 0,0,....,\; \{\backslash \; textbf\; \{b\}\}\; \_\; \{n\},\; 0,0]\}$

Свертка сигнала $x\; \{\backslash \; displaystyle\; \{\backslash \; textbf\; \{x\}\}\}$с функцией прямоугольника $h\; =\; [1/3,\; 1/3,\; 1/3]\; \{\backslash \; displaystyle\; \{\backslash \; textbf\; \{h\}\}\; =\; [1\; /\; 3,1\; /\; 3,1\; /\; 3]\}$дает интерполированные значения b-сплайна первого порядка. B-сплайновая интерполяция второго порядка - это свертка с функцией прямоугольника дважды $y\; =\; x\; \ast \; h\; \ast \; h\; \{\backslash \; displaystyle\; \{\backslash \; textbf\; \{y\}\}\; =\; \{\backslash \; textbf\; \{x\}\}\; *\; \{\backslash \; textbf\; \{h\}\}\; *\; \{\backslash \; textbf\; \{h\}\}\}$, путем итеративной фильтрации с помощью прямоугольной функции получается интерполяция более высокого порядка.

Быстрая интерполяция b-сплайном на однородной области выборки может быть выполнена с помощью итеративной фильтрации среднего значения. В качестве альтернативы функция прямоугольника равна Sinc в области Фурье. Следовательно, интерполяция кубическим сплайном равняется умножению сигнала в области Фурье на Sinc ^ 4.

См. Распределение Ирвина – Холла # Особые случаи для алгебраических выражений для кардинальных B-сплайнов степени 1-4.

P-сплайн

Термин P-spline означает «B-сплайн с ограничениями». Это относится к использованию B-сплайнового представления, в котором коэффициенты определяются частично данными, которые должны быть подобраны, а частично дополнительной функцией штрафа , которая направлена ​​на обеспечение гладкости, чтобы избежать переобучения.

Дву- и многомерные P-сплайновые аппроксимации данных могут использовать произведение граней матриц для минимизации вычислительных операций.

Производная B-сплайна степени k является просто функцией B-сплайнов степени k-1.

$d\; B\; i,\; k\; (x)\; dx\; =\; k\; (B\; i,\; k\; -\; 1\; (Икс)\; Ти\; +\; К\; -\; Ти\; -\; В\; я\; +\; 1,\; К\; -\; 1\; (Икс)\; Ти\; +\; К\; +\; 1\; -\; Ти\; +\; 1)\; \{\backslash \; Displaystyle\; \{\backslash \; гидроразрыва\; \{дБ\_\; \{я,\; к\}\; (х)\}\; \{\; dx\}\}\; =\; k\; \backslash \; left\; (\{\backslash \; frac\; \{B\_\; \{i,\; k-1\}\; (x)\}\; \{t\_\; \{i\; +\; k\}\; -t\_\; \{i\}\}\}\; -\; \{\backslash \; frac\; \{B\_\; \{i\; +\; 1,\; k\; -1\}\; (x)\}\; \{t\_\; \{i\; +\; k\; +\; 1\}\; -t\_\; \{i\; +\; 1\}\}\}\; \backslash \; right)\}$

Отсюда следует, что

$ddx\; \sum \; i\; \alpha \; i\; B\; i,\; k\; =\; \sum \; i\; =\; r\; -\; k\; +\; 2\; s\; -\; 1\; k\; \alpha \; i\; -\; \alpha \; i\; -\; 1\; ti\; +\; k\; -\; ti\; B\; i,\; k\; -\; 1\; на\; [tr.\; ts]\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\}\; \{dx\}\}\; \backslash \; sum\; \_\; \{i\}\; \backslash \; alpha\; \_\; \{i\}\; B\_\; \{i,\; k\}\; =\; \backslash \; sum\; \_\; \{i\; =\; r-k\; +\; 2\}\; ^\; \{s-\; 1\}\; k\; \{\backslash \; frac\; \{\backslash \; alpha\; \_\; \{i\}\; -\; \backslash \; alpha\; \_\; \{i-1\}\}\; \{t\_\; \{i\; +\; k\}\; -t\_\; \{i\}\}\}\; B\_\; \{i,\; k-1\}\; \backslash \; on\; [t\_\; \{\; r\}.t\_\; \{s\}]\}$

который показывает, что существует простая взаимосвязь между производной сплайновой функции и B-сплайнами степени на единицу меньше.

Одномерные B-сплайны, т. Е. B-сплайны, где положения узлов лежат в одном измерении, могут использоваться для представления одномерных функций плотности вероятности $п\; (Икс)\; \{\backslash \; Displaystyle\; р\; (х)\}$. Примером является взвешенная сумма $i\; \{\backslash \; displaystyle\; i\}$базисных функций B-сплайна порядка $n\; \{\backslash \; displaystyle\; n\}$, каждая из которых является областью- нормализовано к единице (т. е. не оценивается напрямую с помощью стандартного алгоритма де-Бура)

$p\; (x)\; =\; \sum \; ici\; \cdot \; B\; i,\; n,\; norm\; (x)\; \{\backslash \; displaystyle\; p\; (x)\; =\; \backslash \; sum\; \_\; \{i\}\; c\_\; \{i\}\; \backslash \; cdot\; B\_\; \{i,\; n,\; \{\backslash \; textbf\; \{norm\}\}\}\; (x)\}$

и с ограничением константы нормализации $\sum \; ici\; =\; 1\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{i\}\; c\_\; \{\; i\}\; =\; 1\}$. K-й необработанный момент $\mu \; k\; \{\backslash \; displaystyle\; \backslash \; mu\; \_\; \{k\}\}$нормализованного B-сплайна $B\; i,\; n,\; norm\; \{\backslash \; displaystyle\; B\_\; \{i,\; n,\; \{\backslash \; textbf\; \{norm\}\}\}\}$можно записать как среднее значение Дирихле Карлсона $R\; k\; \{\backslash \; displaystyle\; R\_\; \{k\}\}$, которое, в свою очередь, может быть решено точно с помощью контурного интеграла и итерационной суммы как

$\mu \; k\; =\; R\; k\; (m;\; t)\; =\; \int \; -\; \infty \; \infty \; xk\; \cdot \; B\; i,\; n,\; norm\; (x\; |\; t\; 1\dots \; tj)\; dx\; =\; \Gamma \; (k\; +\; 1)\; \Gamma \; (м)\; \Gamma \; (м\; +\; К)\; \cdot \; D\; К\; (м,\; t)\; \{\backslash \; displaystyle\; \backslash \; mu\; \_\; \{k\}\; =\; R\_\; \{k\}\; (\backslash \; mathbf\; \{m\};\; \backslash \; mathbf\; \{t\})\; =\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; x\; ^\; \{k\}\; \backslash \; cdot\; B\_\; \{i,\; n,\; \{\backslash \; textbf\; \{norm\}\}\}\; (x\; |\; t\_\; \{1\}\; \backslash \; dots\; t\_\; \{j\})\; dx\; =\; \{\backslash \; frac\; \{\backslash \; Gamma\; (k\; +\; 1)\; \backslash \; Gamma\; (m)\}\; \{\backslash \; Gamma\; (m\; +\; k)\}\}\; \backslash \; cdot\; D\_\; \{k\}\; (\backslash \; mathbf\; \{m\},\; \backslash \; mathbf\; \{t\})\}$

с

$D\; К\; знак\; равно\; 1\; К\; \sum \; U\; знак\; равно\; 1\; К\; [(\sum \; я\; =\; 1\; jmi\; \cdot \; tiu)\; D\; k\; -\; u]\; \{\backslash \; displaystyle\; D\_\; \{k\}\; =\; \{\backslash \; frac\; \{1\}\; \{k\}\}\; \backslash \; sum\; \backslash \; limits\; \_\; \{\; u\; =\; 1\}\; ^\; \{k\}\; \backslash \; left\; [\backslash \; left\; (\backslash \; sum\; \backslash \; limits\; \_\; \{i\; =\; 1\}\; ^\; \{j\}\; m\_\; \{i\}\; \backslash \; cdot\; \{t\_\; \{i\}\}\; ^\; \{u\}\; \backslash \; right)\; D\_\; \{ку\; \}\; \backslash \; right]\}$

и $D\; 0\; =\; 1\; \{\backslash \; displaystyle\; D\_\; \{0\}\; =\; 1\}$. Здесь $t\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{t\}\}$представляет вектор с $j\; \{\backslash \; displaystyle\; j\}$положениями узлов и $m\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{m\}\}$вектор с соответствующими кратностями узлов. Следовательно, можно точно вычислить любой момент функции плотности вероятности $p\; (x)\; \{\backslash \; displaystyle\; p\; (x)\}$, представленной суммой базисных функций B-сплайна, не прибегая к численным методам.

A Кривая Безье также является полиномиальной кривой, определяемой с использованием рекурсии из кривых более низкой степени того же класса и закодированной в терминах контрольных точек, но ключевое отличие заключается в что все термины в рекурсии для сегмента кривой Безье имеют одну и ту же область определения (обычно $[0,\; 1]\; \{\backslash \; displaystyle\; [0,1]\}$), тогда как поддерживает двух членов в B-сплайн-рекурсии различны (крайние подынтервалы не являются общими). Это означает, что кривая Безье степени $n\; \{\backslash \; displaystyle\; n\}$, заданная как $m\; \gg \; n\; \{\backslash \; displaystyle\; m\; \backslash \; gg\; n\}$, контрольные точки состоят примерно из $m\; /\; n\; \{\backslash \; displaystyle\; m\; /\; n\}$в основном независимые сегменты, тогда как B-сплайн с теми же параметрами плавно переходит от подынтервала к подинтервалу. Чтобы получить что-то сопоставимое с кривой Безье, нужно наложить условие гладкости на переходы между сегментами, что приведет к некоторому виду сплайна Безье (для которого многие контрольные точки будут определяться требованием гладкости).

A кусочно / составная кривая Безье представляет собой серию кривых Безье, соединенных по крайней мере с непрерывностью C0 (последняя точка одной кривой совпадает с начальной точкой следующей кривой). В зависимости от приложения могут быть добавлены дополнительные требования к гладкости (например, непрерывность C1 или C2). Непрерывные кривые C1 имеют идентичные касательные в точке излома (где встречаются две кривые). Непрерывные кривые C2 имеют одинаковую кривизну в точке излома.

Чтобы получить непрерывность C2, кривая Безье теряет локальный контроль, потому что для обеспечения непрерывности C2 контрольные точки зависят друг от друга. Если перемещается одна контрольная точка, необходимо повторно оценить весь сплайн. B-сплайны имеют как непрерывность C2, так и локальное управление, но они теряют свойство интерполяции кусочного Безье.

Обычно в подгонке кривой, набор точки данных соответствуют кривой, определяемой некоторой математической функцией. Например, обычные типы аппроксимации кривой используют полином или набор экспоненциальных функций. Когда нет теоретической основы для выбора функции аппроксимации, кривая может быть аппроксимирована сплайновой функцией, составленной из суммы B-сплайнов, с использованием метода наименьших квадратов. Таким образом, целевая функция минимизации методом наименьших квадратов для сплайновой функции степени k:

$U\; =\; \sum \; allx\; \{W\; (x)\; [y\; (x)\; -\; \sum \; i\; \alpha \; i\; B\; i,\; к,\; t\; (x)]\}\; 2\; \{\backslash \; displaystyle\; U\; =\; \backslash \; sum\; \_\; \{\backslash \; mathrm\; \{all\}\; \backslash ,\; x\}\; \backslash \; left\; \backslash \; \{W\; (x)\; \backslash \; left\; [y\; (x)\; -\; \backslash \; sum\; \_\; \{i\}\; \backslash \; alpha\; \_\; \{i\}\; B\_\; \{i,\; k,\; t\}\; (x)\; \backslash \; right]\; \backslash \; right\; \backslash \}\; ^\; \{2\}\}$

W (x) - это вес, а y (x) - это значение в точке x. Коэффициенты $\alpha \; i\; \{\backslash \; displaystyle\; \backslash \; alpha\; \_\; \{i\}\}$- это параметры, которые необходимо определить. Значения узлов могут быть фиксированными или их также можно рассматривать как параметры.

Основная трудность при применении этого процесса заключается в определении количества используемых узлов и их расположения. де Бур предлагает различные стратегии решения этой проблемы. Например, расстояние между узлами уменьшается пропорционально кривизне (2-я производная) данных. Было опубликовано несколько приложений. Например, было исследовано использование B-сплайнов для аппроксимации одиночных кривых лоренцевой и гауссовой кривых. Рассчитаны оптимальные сплайн-функции степеней 3-7 включительно, основанные на симметричном расположении узлов 5, 6 и 7 узлов, и метод применен для сглаживания и дифференцирования спектроскопических кривых. В сопоставимом исследовании двумерная версия фильтрации Савицкого-Голея и сплайн-метода дали лучшие результаты, чем скользящее среднее или фильтрация Чебышева.

В приложениях автоматизированного проектирования и компьютерной графики сплайн-кривая иногда представляется как $C\; (t)\; \{\backslash \; displaystyle\; C\; (t)\}$, параметрическая кривая некоторого реального параметра $t\; \{\backslash \; displaystyle\; t\}$. В этом случае кривая $C\; (t)\; \{\backslash \; displaystyle\; C\; (t)\}$может рассматриваться как две или три отдельные координатные функции $(x\; (t),\; y\; (t))\; \{\backslash \; Displaystyle\; (х\; (т),\; у\; (т))\}$или $(х\; (т),\; у\; (т),\; г\; (т))\; \{\backslash \; Displaystyle\; (х\; (т),\; y\; (t),\; z\; (t))\}$. Координатные функции $x\; (t)\; \{\backslash \; displaystyle\; x\; (t)\}$, $y\; (t)\; \{\backslash \; displaystyle\; y\; (t)\}$и $z\; (t)\; \{\backslash \; displaystyle\; z\; (t)\}$- каждая сплайн-функция с общим набором узловых значений $t\; 1,\; t\; 2,\dots ,\; tn\; \{\backslash \; displaystyle\; t\_\; \{1\},\; t\_\; \{2\},\; \backslash \; ldots,\; t\_\; \{n\}\}$.

Поскольку B-сплайны образуют базисные функции, каждая из координатных функций может быть выражена как линейная сумма B-сплайнов, поэтому мы имеем

$X\; (t)\; =\; \sum \; ixi\; B\; i,\; n\; (t),\; Y\; (t)\; =\; \sum \; iyi\; B\; i,\; n\; (t),\; Z\; (t)\; =\; \sum \; izi\; B\; i,\; n\; (t).\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{выровнено\}\; X\; (t)\; =\; \backslash \; sum\; \_\; \{i\}\; x\_\; \{i\}\; B\_\; \{i,\; n\}\; (t),\; \backslash \backslash \; Y\; (t)\; =\; \backslash \; sum\; \_\; \{i\}\; y\_\; \{i\}\; B\_\; \{i,\; n\}\; (t),\; \backslash \backslash \; Z\; (t)\; =\; \backslash \; sum\; \_\; \{i\}\; z\_\; \{i\}\; B\_\; \{i,\; n\}\; (t).\; \backslash \; end\; \{align\}\}\}$

Веса $xi\; \{\backslash \; displaystyle\; x\_\; \{i\}\}$, $yi\; \{\backslash \; displaystyle\; y\_\; \{i\}\}$и $zi\; \{\backslash \; displaystyle\; z\_\; \{i\}\}$можно объединить в точки $P\; i\; =\; (xi,\; yi,\; zi)\; \{\backslash \; displaystyle\; P\_\; \{i\}\; =\; (x\_\; \{i\},\; y\_\; \{i\},\; z\_\; \{i\})\}$в 3-м пространстве. Эти точки $P\; i\; \{\backslash \; displaystyle\; P\_\; \{i\}\}$обычно известны как контрольные точки.

Работая в обратном порядке, последовательность контрольных точек, значений узлов и порядка B-сплайна определяет параметрическую кривую. Это представление кривой с помощью контрольных точек имеет несколько полезных свойств:

1. Контрольные точки $P\; i\; \{\backslash \; displaystyle\; P\_\; \{i\}\}$определяют кривую. Если все контрольные точки каким-либо образом трансформируются вместе, например, перемещаются, вращаются, масштабируются или перемещаются с помощью любого аффинного преобразования, тогда соответствующая кривая трансформируется таким же образом.
2. Поскольку B-сплайны отличны от нуля только для конечного числа узловых интервалов, если одна контрольная точка перемещается, соответствующее изменение параметрической кривой находится чуть выше диапазона параметров небольшого числа узловых интервалов.
3. Потому что $\sum \; я\; B\; i,\; n\; (x)\; =\; 1\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{i\}\; B\_\; \{i,\; n\}\; (x)\; =\; 1\}$, и всегда каждый $B\; i,\; n\; (x)\; \ge \; 0\; \{\backslash \; displaystyle\; B\_\; \{i,\; n\}\; (x)\; \backslash \; geq\; 0\}$, тогда кривая остается внутри ограничивающей рамки контрольных точек. Кроме того, в некотором смысле кривая в целом следует за контрольными точками.

Менее желательной особенностью является то, что параметрическая кривая не интерполирует контрольные точки. Обычно кривая не проходит через контрольные точки.

NURBS-кривая - полиномиальная кривая, определенная в однородных координатах (синий) и ее проекция на плоскость - рациональная кривая (красный)

В автоматизированном проектировании, автоматизированное производство и компьютерная графика, мощным расширением B-сплайнов являются неоднородные рациональные B-сплайны (NURBS). NURBS - это, по сути, B-сплайны в однородных координатах. Как и B-сплайны, они определяются своим порядком, вектором узла и набором контрольных точек, но, в отличие от простых B-сплайнов, каждая контрольная точка имеет вес. Когда вес равен 1, NURBS представляет собой просто B-сплайн, и, как таковой, NURBS обобщает как B-сплайны, так и кривые Безье и поверхности, основное различие заключается во взвешивании контрольных точек, что делает NURBS кривые "рациональные".

Оценивая NURBS при различных значениях параметров, кривую можно проследить в пространстве; аналогично, оценивая NURBS-поверхность при различных значениях двух параметров, поверхность может быть представлена ​​в декартовом пространстве.

Подобно B-сплайнам, контрольные точки NURBS определяют форму кривой. Каждая точка кривой вычисляется путем взвешивания суммы нескольких контрольных точек. Вес каждой точки зависит от управляющего параметра. Для кривой степени d влияние любой контрольной точки ненулевое только в d + 1 интервалах (узлах) пространства параметров. В пределах этих интервалов вес изменяется в соответствии с полиномиальной функцией (базисными функциями) степени d. На границах интервалов базисные функции плавно уходят в нуль, причем гладкость определяется степенью полинома.

Узловой вектор - это последовательность значений параметров, которая определяет, где и как контрольные точки влияют на кривую NURBS. Количество узлов всегда равно количеству контрольных точек плюс градус кривой плюс один. Каждый раз, когда значение параметра входит в новый диапазон узлов, новая контрольная точка становится активной, а старая контрольная точка отбрасывается.

NURBS-кривая имеет следующий вид:

$C\; (u)\; =\; \sum \; i\; =\; 1\; k\; N\; i,\; nwi\; P\; i\; \sum \; i\; =\; 1\; k\; N\; i,\; nwi\; \{\backslash \; displaystyle\; C\; (u)\; =\; \{\backslash \; frac\; \{\backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{k\}\; \{N\_\; \{i,\; n\}\; w\_\; \{i\}\; P\}\; \_\; \{i\}\}\; \{\backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{k\}\; \{N\_\; \{\; i,\; n\}\; w\_\; \{i\}\}\}\}\}$

Здесь обозначения следующие. u - независимая переменная (вместо x), k - количество контрольных точек, N - это B-сплайн (используется вместо B), n - степень полинома, P - контрольная точка, а w - вес. Знаменатель - это нормализующий коэффициент, который дает единицу, если все веса равны единице.

Обычно это пишут как

$C\; (u)\; =\; \sum \; i\; =\; 1\; k\; R\; i,\; n\; (u)\; P\; i\; \{\backslash \; displaystyle\; C\; (u)\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\; \}\; ^\; \{k\}\; R\_\; \{i,\; n\}\; (u)\; P\_\; \{i\}\}$

, в котором функции

$R\; i,\; n\; (u)\; =\; N\; i,\; n\; (u)\; wi\; \sum \; j\; =\; 1\; k\; N\; J,\; N\; (U)\; WJ\; \{\backslash \; Displaystyle\; R\_\; \{I,\; N\}\; (U)\; =\; \{N\_\; \{I,\; N\}\; (U)\; W\_\; \{I\}\; \backslash \; over\; \backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{k\}\; N\_\; \{j,\; n\}\; (u)\; w\_\; \{j\}\}\}$

известны как рациональные базисные функции.

NURBS-поверхность получается как тензорное произведение двух NURBS-кривых с использованием двух независимых параметров u и v (с индексами i и j соответственно):

$S\; (u,\; v)\; знак\; равно\; \sum \; я\; знак\; равно\; 1\; К\; \sum \; J\; знак\; равно\; 1\; l\; р\; я,\; j\; (u,\; v)\; п\; я,\; j\; \{\backslash \; displaystyle\; S\; (u,\; v)\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{k\}\; \backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{l\}\; R\_\; \{i,\; j\}\; (u,\; v)\; P\_\; \{i,\; j\}\}$

с

$R\; i,\; j\; (u,\; v)\; =\; N\; i,\; n\; (\; u)\; N\; j,\; m\; (v)\; wi,\; j\; \sum \; p\; =\; 1\; К\; \sum \; q\; =\; 1\; l\; N\; p,\; n\; (u)\; N\; q,\; m\; (v)\; wp,\; q\; \{\backslash \; displaystyle\; R\_\; \{i,\; j\}\; (u,\; v)\; =\; \{\backslash \; frac\; \{N\_\; \{i,\; n\}\; (u)\; N\_\; \{j,\; m\}\; (v)\; w\_\; \{i,\; j\}\}\; \{\backslash \; sum\; \_\; \{p\; =\; 1\}\; ^\; \{k\}\; \backslash \; sum\; \_\; \{\; q\; =\; 1\}\; ^\; \{l\}\; N\_\; \{p,\; n\}\; (u)\; N\_\; \{q,\; m\}\; (v)\; w\_\; \{p,\; q\}\}\}\}$

как рациональные базисные функции.

• Кривая Безье
• Прямоугольный сплайн
• Алгоритм Де Бура
• I-сплайн
• M-сплайн
• Сплайн вейвлет
• Т-сплайн

Цитированные работы

• Карл де Бур (1978). Практическое руководство по сплайнам. Springer-Verlag. ISBN 978-3-540-90356-7.
• Пигль, Лес; Тиллер, Уэйн (1997). Книга NURBS (2-е изд.). Springer. ISBN 978-3-540-61545-3.

• Ричард Х. Бартельс; Джон С. Битти; Брайан А. Барский (1987). Введение в сплайны для использования в компьютерной графике и геометрическом моделировании. Морган Кауфманн. ISBN 978-1-55860-400-1.
• Жан Галлье (1999). Кривые и поверхности в геометрическом моделировании: теория и алгоритмы. Морган Кауфманн. Глава 6. Кривые B-сплайна. Эта книга больше не издается и находится в свободном доступе у автора.
• Хартмут Праутч; Вольфганг Бём; Марко Палушны (2002). Безье и методы B-сплайна. Springer Science Business Media. ISBN 978-3-540-43761-1.
• Дэвид Саломон (2006). Кривые и поверхности для компьютерной графики. Springer. Глава 7. B-сплайновая аппроксимация. ISBN 978-0-387-28452-1.

• Вайсштейн, Эрик У. "B-Spline". MathWorld.
• Руф, Йоханнес. «B-шлицы третьего порядка на неоднородной сетке» (PDF). Архивировано из оригинального (PDF) от 06.11.2013. Получено 2 мая 2012 г.
• двумерный B-сплайн из numpy
• Интерактивные B-сплайны с JSXGraph
• TinySpline: C-библиотека с открытым исходным кодом с привязками для различных языков
• Унифицированные нерациональные B-сплайны, моделирование кривые в 2D пространстве. Автор: Стефан Г. Бек
• Редактор B-Spline, автор Шукант Пал