В математике, автономная система или автономный дифференциал уравнение представляет собой систему из обыкновенных дифференциальных уравнений, которая явно не зависит от независимой переменной. Когда переменная - время, они также называются инвариантными во времени системами.
. Выражены многие законы физики, где независимой переменной обычно считается время. как автономные системы, потому что предполагается, что законы природы, действующие сейчас, идентичны законам в любой момент в прошлом или будущем.
Автономные системы тесно связаны с динамическими системами. Любая автономная система может быть преобразована в динамическую систему, и, используя очень слабые предположения, динамическая система может быть преобразована в автономную систему.
Содержание
- 1 Определение
- 2 Свойства
- 3 Пример
- 4 Качественный анализ
- 5 Методы решения
- 5.1 Первый порядок
- 5.2 Второй порядок
- 5.2.1 Специальные case: x '' = f (x)
- 5.2.2 Особый случай: x '' = x 'f (x)
- 5.3 Высшие порядки
- 6 См. также
- 7 Ссылки
Определение
Автономная система - это система обыкновенных дифференциальных уравнений в форме

где x принимает значения в n-мерном евклидовом пространстве ; t часто интерпретируется как время.
Он отличается от систем дифференциальных уравнений вида

, в котором закон, регулирующий эволюцию системы, зависит не только от текущего состояния системы, но и от параметра t, который также часто интерпретируется как время; такие системы по определению не являются автономными.
Свойства
Пусть  будет уникальным решением начального значения проблема для автономной системы
будет уникальным решением начального значения проблема для автономной системы
 .
.
Тогда  решает
решает
 .
.
Действительно, обозначая  , мы имеем
, мы имеем  и
и  , таким образом,
, таким образом,
 .
.
Для начального условия проверкой является tr ivial,
 .
.
Пример
Уравнение  является автономным, поскольку независимая переменная, назовем ее
является автономным, поскольку независимая переменная, назовем ее  , явно не появляется в уравнение. Чтобы построить поле наклона и изоклина для этого уравнения, можно использовать следующий код в GNU Octave / MATLAB
, явно не появляется в уравнение. Чтобы построить поле наклона и изоклина для этого уравнения, можно использовать следующий код в GNU Octave / MATLAB
Ffun = @ ( X, Y) (2 - Y). * Y; % function f (x, y) = (2-y) y [X, Y] = meshgrid (0:.2: 6, - 1:.2: 3); % выберите размеры графика DY = Ffun (X, Y); DX = единицы (размер (DY)); % генерировать колчан значений графика (X, Y, DX, DY, 'k'); % построить поле направления черным цветом; контур (X, Y, DY, [0 1 2], 'g'); % добавить изоклины (0 1 2) в зеленый заголовок ('Поле наклона и изоклины для f (x, y) = (2-y) y')Из графика видно, что функция 
 -инвариантно, как и форма решения, т. Е.
-инвариантно, как и форма решения, т. Е.  для любого сдвига
для любого сдвига  .
.
Символьное решение уравнения в MATLAB путем выполнения
y = dsolve ('Dy = (2-y) * y', 'x'); % решая уравнение символически, получаем два равновесных решения,  и
и  , и третье решение с неизвестной константой
, и третье решение с неизвестной константой  ,
,
y (3) = - 2 / (exp (C3 - 2 * x) - 1)
Взяв некоторые конкретные значения для начального условия, мы можем добавить график нескольких решений
y1 = dsolve ('Dy = (2-y) * y', 'у (1) = 1', 'х'); % решить задачу начального значения символически y2 = dsolve ('Dy = (2-y) * y', 'y (2) = 1', 'x'); % для разных начальных условий y3 = dsolve ('Dy = (2-y) * y', 'y (3) = 1', 'x'); у4 = dsolve ('Dy = (2-y) * y', 'y (1) = 3', 'x'); y5 = dsolve ('Dy = (2-y) * y', 'y (2) = 3', 'x'); y6 = dsolve ('Dy = (2-y) * y', 'y (3) = 3', 'x'); ezplot (y1, [0 6]); ezplot (y2, [0 6]); % построить решения ezplot (y3, [0 6]); ezplot (y4, [0 6]); ezplot (y5, [0 6]); ezplot (y6, [0 6]); title ('Поле уклона, изоклины и решения для f (x, y) = (2-y) y') legend ('Поле уклона', 'Изоклины', 'Решения y_ {1..6}'); текст ([1 2 3], [1 1 1], strcat ('\ leftarrow', {'y_1', 'y_2', 'y_3'})); текст ([1 2 3], [3 3 3], strcat ('\ leftarrow', {'y_4', 'y_5', 'y_6'})); сетка включена;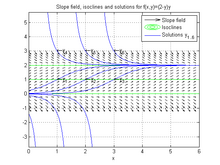
Поле наклона с изоклинами и решениями
Качественный анализ
Автономные системы могут быть проанализированы качественно с помощью фазового пространства ; в случае одной переменной это фазовая линия .
Методы решения
Следующие методы применяются к одномерным автономным дифференциальным уравнениям. Любое одномерное уравнение порядка  эквивалентно
эквивалентно  -мерной системе первого порядка (как описано in Обычное дифференциальное уравнение # Редукция к системе первого порядка ), но не обязательно наоборот.
-мерной системе первого порядка (как описано in Обычное дифференциальное уравнение # Редукция к системе первого порядка ), но не обязательно наоборот.
Первый порядок
Автономное уравнение первого порядка

является разделимым, поэтому его легко решить, преобразовав его в интегральную форму

Второй порядок
Автономное уравнение второго порядка

сложнее, но его можно решить, введя новую переменную

и выражая вторую производную от  (через правило цепочки ) как
(через правило цепочки ) как

, так что исходное уравнение принимает вид

который является уравнением первого порядка uation не содержит ссылки на независимую переменную  и, если решено, предоставляет
и, если решено, предоставляет  как функцию от
как функцию от  . Затем, вспоминая определение
. Затем, вспоминая определение  :
:

, которое является неявным решением.
Особый случай: x '' = f (x)
Особый случай, когда  не зависит от
не зависит от 

преимущества из отдельного обращения. Эти типы уравнений очень распространены в классической механике, потому что они всегда являются гамильтоновыми системами.
Идея состоит в том, чтобы использовать тождество (исключая деление на ноль )

который следует из правила цепочки . Отметим в стороне, что, инвертируя обе стороны автономной системы первого порядка, можно немедленно интегрировать по  :
:

, что является еще одним способом взглянуть на технику разделения переменных. Тогда возникает естественный вопрос: можем ли мы сделать что-то подобное с уравнениями более высокого порядка? Ответ положительный для уравнений второго порядка, но есть над чем поработать. Вторая производная должна быть выражена как производная по отношению к  вместо
вместо  :
:

Чтобы еще раз подчеркнуть: достигнуто то, что вторая производная в  есть пчела n, выраженное как производная в
есть пчела n, выраженное как производная в  . Затем исходное уравнение второго порядка может быть окончательно интегрировано:
. Затем исходное уравнение второго порядка может быть окончательно интегрировано:





Это неявное решение, и помимо этого самая большая потенциальная проблема - невозможность упростить интегралы, что подразумевает трудность или невозможность вычисления констант интегрирования.
Особый случай: x '' = x 'f (x)
Используя вышеупомянутый подход, мы можем расширить метод до более общего уравнения

, где  - некоторый параметр, не равный двум. Это будет работать, поскольку вторая производная может быть записана в форме, включающей степень
- некоторый параметр, не равный двум. Это будет работать, поскольку вторая производная может быть записана в форме, включающей степень  . Переписываем вторую производную, переставляем и выражаем левую часть как производную:
. Переписываем вторую производную, переставляем и выражаем левую часть как производную:





Справа будет +/-, если  четное. Обработка должна быть другой, если
четное. Обработка должна быть другой, если  :
:




высшие порядки
Аналогового метода решения автономных уравнений третьего и более высокого порядка не существует. Такие уравнения могут быть решены точно только в том случае, если они обладают каким-либо другим упрощающим свойством, например, линейностью или зависимостью правой части уравнения только от зависимой переменной (т. Е. Не от ее производных). Это не должно вызывать удивления, учитывая, что нелинейные автономные системы в трех измерениях могут производить поистине хаотическое поведение, такое как аттрактор Лоренца и аттрактор Ресслера.
. Также неудивительно, что общие неавтономные уравнения второго порядка не могут быть решены явно, поскольку они также могут быть хаотическими (примером этого является периодически вынужденный маятник).
См. Также
Ссылки



 .
.
 .
.


 .
. .
.







 Поле наклона с изоклинами и решениями
Поле наклона с изоклинами и решениями 









































